¿Cómo encontrar los momentos de la distribución geométrica
Momentos
Conteúdo
El número de ensayos requiere antes de que el primer éxito se lleva a cabo
El número de fallos que se producen antes de que el primer éxito
Al igual que con la distribución binomial, la distribución geométrica tiene una serie de fórmulas simplificadas para el cálculo de estos momentos.
Cómo calcular el valor esperado de la distribución geométrica
El valor esperado de la distribución geométrica cuando se determina el número de ensayos necesarios hasta que el primer éxito es
El valor esperado de la distribución geométrica cuando se determina el número de errores que se producen antes de que el primer éxito es
Por ejemplo, al voltear las monedas, si el éxito se define como "una cabeza aparece," la probabilidad de un éxito es igual p = 0.5-, por lo tanto, el fracaso se define como "una colas convierte en imagen" y 1 - p = 1 - 0,5 = 0,5. En promedio, habrá (1 - p) /p = (1-0,5) /0.5 = 0,5 / 0,5 = 1 colas antes de las primeras cabezas aparece.
Observe cómo los dos resultados proporcionan la misma detallada que se necesita un promedio de dos lanzamientos para conseguir los primeros jefes, o en promedio debe haber una cola antes de las primeras cabezas vueltas hacia arriba.
Cómo calcular la varianza y la desviación estándar de la distribución geométrica
La desviación estándar de la varianza y de la distribución geométrica para determinar el número de ensayos necesarios hasta que el primer éxito o al determinar el número de errores que se producen antes de que el primer éxito son
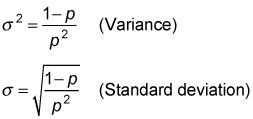
Por ejemplo, supongamos que usted lanza una moneda hasta que los primeros cabezas vueltas hacia arriba. El número esperado de los ensayos necesarios hasta que los primeros cabezas convierte en imagen es
La varianza es
-
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
La distribución chi-cuadrado en la econometría -
Diferenciar entre distribuciones de probabilidad discretas y continuas -
Cómo el número de grados de libertad afecta a la gráfica de una distribución t -
Cómo calcular las probabilidades geométricas -
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t
Cómo calcular la varianza y la desviación estándar en la distribución uniforme los distribución uniforme se utiliza para describir una situación en la que todos los posibles resultados de un experimento aleatorio tienen la misma probabilidad de ocurrir. Puede utilizar la varianza y la desviación estándar para medir el…
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
Cómo calcular las probabilidades de Poisson los Distribución de Poisson es útil para medir cómo pueden ocurrir muchos eventos durante un horizonte de tiempo dado, tal como el número de clientes que entran en una tienda durante la siguiente hora, el número de accesos a una página web…
¿Cómo encontrar percentiles de una distribución t Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…
¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
Cómo graficar la distribución binomial Una forma de ilustrar la distribución binomial es con un histograma. Un histograma muestra los valores posibles de una distribución de probabilidad como una serie de barras verticales. La altura de cada barra refleja la probabilidad de cada valor…
Cómo identificar una variable aleatoria binomial La variable aleatoria discreta más conocido y amado en las estadísticas es el binomio. Binomial medio dos nombres y se asocia con situaciones que participen dos resultados- por ejemplo, sí / no, o el éxito / fracaso (golpear una luz roja o no,…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
Cómo saber cuando una variable aleatoria no tiene una distribución binomial Con el fin de saber cuándo una variable aleatoria de una muestra estadística no tiene una distribución binomial, primero tiene que saber lo que hace que sea binomial. Puede identificar una variable aleatoria binomial como si se cumplen las cuatro…
Cómo utilizar el operador de suma para calcular el valor esperado Las propiedades de una distribución de probabilidad se pueden resumir con un conjunto de medidas numéricas conocidas como momentos. Uno de estos momentos se llama valor esperado, o media. Para el cálculo de un valor esperado, se utiliza un…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…