Cómo utilizar el operador de suma para calcular el valor esperado
Las propiedades de una distribución de probabilidad se pueden resumir con un conjunto de medidas numéricas conocidas como momentos. Uno de estos momentos se llama valor esperado, o media. Para el cálculo de un valor esperado, se utiliza un operador de suma.
El operador suma se utiliza para indicar que un conjunto de valores debe añadirse juntos. Las fórmulas utilizadas para calcular los momentos de una distribución de probabilidad se basan en el operador de suma. Esto se debe a que cada cálculo debe repetirse para cada posible valor de una variable aleatoria y los resultados deben ser resumida.
Como un ejemplo de que el operador de suma, supone un conjunto de datos contiene cinco elementos. El operador sumatoria le dice que lleve a cabo los siguientes cálculos:
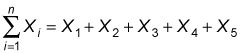
Xyo representa un solo elemento en un ajuste de datos yo es un índice, y n es el número de elementos para resumir.
los valor esperado de una variable aleatoria X representa el valor promedio de X que se produce si el experimento aleatorio se repite un gran número de veces. Usted puede pensar en el valor esperado como el centro de la distribución.
El valor esperado es una peso promedio de sus valores posibles, con pesos iguales a las probabilidades. La fórmula para el cálculo del valor esperado X es
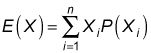
Estos son los términos clave en esta fórmula:
E (X) = El valor esperado de X
n = El número de valores posibles de X
yo = Un índice
Xi = Un valor posible de X
P (Xi) = La probabilidad de Xi
Supongamos que una empresa biofarmacéutica está planeando lanzar varios medicamentos nuevos durante el año que viene, en función de si o no se aprueban las patentes. Puede utilizar la variable aleatoria X para representar el número de nuevos fármacos que se dará a conocer.
La tabla muestra la distribución de probabilidad de los resultados.
| X | P (X) |
|---|---|
| 0 | 0.10 |
| 1 | 0.25 |
| 2 | 0.50 |
| 3 | 0.15 |
A continuación, puede utilizar la distribución de probabilidad para determinar la (promedio) valor esperado de X mediante el establecimiento de los valores posibles de X y las probabilidades correspondientes, así:
X1 = 0 P(X1) = 0,10
X2 = 1 P(X2) = 0,25
X3 = 2 P(X3) = 0,50
X4 = 3 P(X4) = 0,15
El histograma correspondiente se muestra aquí.
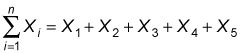
A continuación, sustituir estos números en la fórmula de valor esperado:
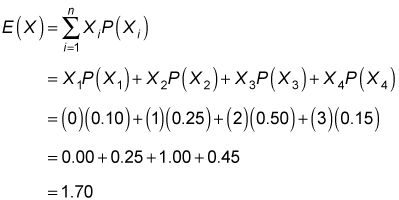
Este resultado muestra que el número (promedio) que se espera de nuevos fármacos que se dará a conocer durante el próximo año es de 1.7. Aunque es físicamente imposible para liberar 1,7 nuevos fármacos (desde 1.7 no es un entero o número entero), si este experimento se repite muchas veces, el número promedio de nuevos fármacos publicada será 1,7.
-
Econometría y la función de densidad acumulativa (CDF) -
Econometría y la función de densidad de probabilidad (pdf) -
Cómo hacer generalizaciones en la econometría con valor esperado o media -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Economía de la empresa: cómo crear el mejor del peor caso -
Diferenciar entre distribuciones de probabilidad discretas y continuas
Cómo calcular las probabilidades geométricas La distribución geométrica se basa en el proceso binomial (una serie de ensayos independientes con dos resultados posibles). Se utiliza la distribución geométrica para determinar la probabilidad de que un determinado número de pruebas se…
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
Cómo calcular las probabilidades de Poisson los Distribución de Poisson es útil para medir cómo pueden ocurrir muchos eventos durante un horizonte de tiempo dado, tal como el número de clientes que entran en una tienda durante la siguiente hora, el número de accesos a una página web…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
¿Cómo encontrar los momentos de la distribución geométrica Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. Los momentos de la distribución geométrica depende de cuál de las siguientes situaciones se está…
Cómo graficar la distribución binomial Una forma de ilustrar la distribución binomial es con un histograma. Un histograma muestra los valores posibles de una distribución de probabilidad como una serie de barras verticales. La altura de cada barra refleja la probabilidad de cada valor…
Cómo indicar posibles resultados de una variable aleatoria discreta Una variable aleatoria discreta X puede tomar en un determinado conjunto de resultados posibles, y cada uno de esos resultados tiene una cierta probabilidad estadística de que se produzcan. La notación utilizada para cualquier resultado…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
Variables aleatorias y distribuciones de probabilidad en las estadísticas empresariales Variables aleatorias y distribuciones de probabilidad son dos de los conceptos más importantes en las estadísticas. LA variable al azar asigna valores numéricos únicos para los resultados de un experimento- azar este es un proceso que genera…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…
Distribuciones de probabilidad continuas Cuando se trabaja con distribuciones de probabilidad continuas, las funciones pueden tomar muchas formas. Estos incluyen uniforme continua, exponencial, normal, normal estándar (Z), la aproximación binomial, Poisson aproximación, y distribuciones…