La distribución chi-cuadrado en la econometría
En econometría, se utiliza la distribución chi-cuadrado ampliamente. La distribución chi-cuadrado es útil para comparar los valores de varianza estimada de una muestra a esos valores basados en supuestos teóricos. Por lo tanto, se utiliza normalmente para desarrollar intervalos de confianza y pruebas de hipótesis para la varianza de la población. En primer lugar, sin embargo, usted debe familiarizarse con las características de una distribución chi cuadrado.
La distribución chi-cuadrado es una cuadrado normal estándar variable aleatoria, por lo que toma sólo valores no negativos y tiende a estar en lo cierto; sesgada. El alcance de su oblicuidad depende de los grados de libertad o el número de observaciones. Cuanto mayor sea el grado de libertad (más observaciones), el (más simétrica) la distribución chi-cuadrado menos sesgada.
La figura muestra un par de distribuciones chi-cuadrado, donde df1, DF2 y DF3 indican grados crecientes de libertad.
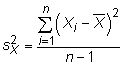
La distribución chi-cuadrado se utiliza típicamente con estimaciones de la varianza y se apoya en la idea de que usted comienza con una variable aleatoria normalmente distribuida, tales como
Con datos de la muestra, a estimar la varianza de esta variable aleatoria con
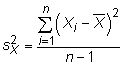
Si algebraicamente manipular esta fórmula, se llega a la distribución chi-cuadrado:
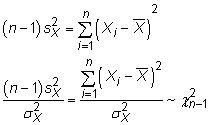
El último paso, en el que se divide ambos lados por lo conocido (o supuesta) varianza de la población, es lo que estandariza la varianza de la muestra a una escala común conocida como chi-cuadrado.
-
¿Cuánto propagación es allí en los datos? -
Distribuciones de probabilidad en el análisis estadístico de datos grande -
Econometría y la distribución t -
Poniendo las variables en la misma escala: la distribución normal estándar (z) -
Reconociendo las variables habituales: distribución normal -
La distribución f en la econometría
Distribuciones de probabilidad discretas y continuas Los dos tipos básicos de las distribuciones de probabilidad se conocen como discreta y continua. Discreta distribuciones describen las propiedades de una variable al azar para los que se asigna cada resultado individual una probabilidad…
Cómo el número de grados de libertad afecta a la gráfica de una distribución t Una de las propiedades interesantes de la distribución t es que cuanto mayor es el grado de libertad, más de cerca la distribución t se asemeja a la distribución normal estándar. A medida que los grados de libertad aumenta, el área en las…
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…
Cómo calcular la varianza y la desviación estándar en la distribución uniforme los distribución uniforme se utiliza para describir una situación en la que todos los posibles resultados de un experimento aleatorio tienen la misma probabilidad de ocurrir. Puede utilizar la varianza y la desviación estándar para medir el…
Cómo calcular los momentos de la distribución de Poisson Al igual que con las distribuciones binomial y geométricas, puede utilizar fórmulas sencillas para calcular los momentos - valor esperado, la varianza y desviación estándar - de la distribución de Poisson.Cómo calcular el valor esperado de la…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…
Variables aleatorias y distribuciones de probabilidad en las estadísticas empresariales Variables aleatorias y distribuciones de probabilidad son dos de los conceptos más importantes en las estadísticas. LA variable al azar asigna valores numéricos únicos para los resultados de un experimento- azar este es un proceso que genera…
Distribuciones estadísticas: binomial, y t-distribución normal Una distribución estadística es una lista de los posibles valores de una variable (o intervalos de valores) y la frecuencia (o en qué densidad) que se produzcan. Se puede tomar varias formas, incluyendo binomial, normal, y t-distribución.LA…