Encuentra las pruebas estadísticas apropiadas para dos poblaciones independientes de igual tamaño y varianza
Puede probar hipótesis acerca de dos medias poblacionales donde las poblaciones son independientes entre sí, pero tienen el mismo tamaño y la varianza. Con igual varianzas poblacionales, la estadística de prueba requiere el cálculo de una variación agrupado - esta es la varianza que las dos poblaciones tienen en común. Se utiliza la distribución t de Student para encontrar la estadística de prueba y los valores críticos.
La elección de la distribución para la prueba de hipótesis sobre la base de muestras independientes se resume en la siguiente tabla:
| Condición | Distribución |
|---|---|
| Varianzas Igualdad | T de Student |
| Varianzas desiguales: al menos una pequeña muestra | T de Student |
| Varianzas desiguales: grandes muestras | Standard Normal (Z) |
Si las varianzas de dos poblaciones son iguales (o se supone que son iguales) la prueba estadística adecuada se basa en la distribución t de Student:
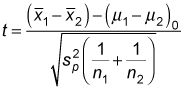
Esto es lo que significa cada término:

Si está llevando a cabo una prueba de hipótesis de dos medias poblacionales con igual varianzas poblacionales, se toma los valores críticos de la distribución t de Student con n1 + n2 - 2 grados de libertad, que le da los siguientes valores fundamentales:

A modo de ejemplo, digamos que una empresa de marketing está interesado en determinar si los hombres y las mujeres son igualmente propensos a comprar un producto nuevo. La empresa elige al azar muestras de hombres y mujeres y les pide que asignar un valor numérico a la probabilidad de que la compra del producto (siendo 1 el menos probable, y 10 es la más probable).
Basado en la experiencia pasada, las varianzas de población se supone que son iguales. El primer paso es asignar un grupo a ser la primera población ("población 1") y el otro grupo para ser la segunda población ("población 2"). La empresa designa a los hombres como la población 1 y mujeres como población 2.
El siguiente paso es elegir las muestras de ambas poblaciones. (Los tamaños de estas muestras no tienen que ser iguales.) Supongamos que la empresa elige muestras de 21 hombres y 21 mujeres. Estas muestras se utilizan para calcular la media de la muestra y muestra la desviación estándar, tanto para hombres como para mujeres.
Supongamos que la media muestral puntuación de los hombres se 7.2- la muestra la puntuación media de las mujeres es de 6.7. También asume que la desviación estándar de la muestra de los hombres es de 0,4 y la desviación estándar de la muestra de las mujeres es de 0,3. Con estos datos en su lugar, la hipótesis nula de que la población puntuaciones medias son iguales está probado por la empresa de marketing al nivel del 5 por ciento de significancia.
Puede resumir los datos de ejemplo, así:
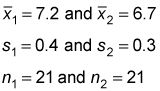
La hipótesis nula es
La hipótesis alternativa es
Para calcular la estadística de prueba, primero calcular la varianza combinado:
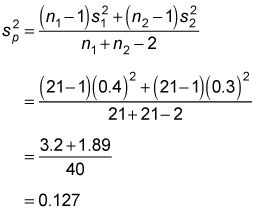
A continuación, sustituir este resultado en la fórmula estadística de prueba:
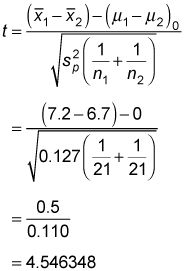
Usted puede encontrar que los valores críticos apropiados de esta tabla (que es un extracto de la tabla t de Student).
| Grados de libertad | t0.10 | t0.05 | t0,025 | t0.01 | t0,005 |
|---|---|---|---|---|---|
| 30 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 |
| 40 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 |
| 60 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 |
Estos se encuentran los siguientes. La fila superior de la tabla t de Student enumera diferentes valores de
donde la cola derecha de la distribución t de Student tiene una probabilidad (área) igual a
En este caso, alfa es 0.05- utilizando un área de la cola de 0,025
y 40 grados de libertad, que encuentran que los valores críticos son:
Debido a que la estadística de prueba (4.546348) supera el valor positivo crítico (2.021), la hipótesis nula
se rechaza.
Con una prueba de dos colas, en realidad hay dos alternativas disponibles para la hipótesis nula:
(es decir, la calificación media de los hombres es mayor que la media entre las mujeres) o
(es decir, la calificación media de los hombres es menor que la media entre las mujeres). En este caso, la estadística de prueba es grande y positiva, lo que sugiere que la media de los hombres es superior a la media para las mujeres. Una estadística de prueba grande y positivo indica que la media de la muestra para los hombres es significativamente mayor que la media muestral para las mujeres. En otras palabras, los hombres son más propensos a comprar el nuevo producto que las mujeres.





