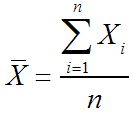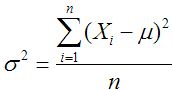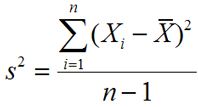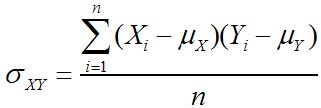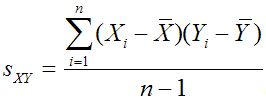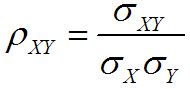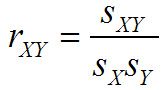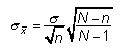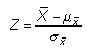Cuando se trabaja con las poblaciones y muestras (un subconjunto de una población) en estadísticas de las empresas, puede utilizar tres tipos comunes de medidas para describir el conjunto de datos: tendencia central, dispersión y asociación.
Por convención, las fórmulas estadísticas que se utilizan para describir las medidas de población contienen letras griegas, mientras que las fórmulas utilizadas para describir las medidas de ejemplo contienen letras latinas.
Medidas de tendencia central
En estadística, la media, la mediana y la moda son conocidos como medidas de tendencia central- que se utilizan para identificar el centro de un conjunto de datos:
La media de: El valor entre los valores mayor y menor de un conjunto de datos, que se obtiene por un método prescrito.
Mediana: El valor que divide un conjunto de datos en dos mitades iguales
Modo: El valor más comúnmente observada en un conjunto de datos
Las muestras se eligen al azar a partir de poblaciones. Si este proceso se lleva a cabo correctamente, cada muestra debe reflejar con precisión las características de la población. Por lo tanto, una medida de la muestra, tales como el significa, debe ser una buena estimación de la medida de población correspondiente. Considere los siguientes ejemplos de media:
Media de la población:
Esta fórmula simplemente le dice al sumar todos los elementos de la población y se dividen por el tamaño de la población.
Media de la muestra:
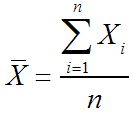
El proceso para calcular esto es exactamente el mismo: se suman todos los elementos de la muestra y se dividen por el tamaño de la muestra.
Además de las medidas de tendencia central, otros dos tipos principales de medidas son medidas de dispersión (spread) y medidas de asociación.
Medidas de dispersión
Medidas de dispersión incluir varianza / desviación estándar y percentiles / cuartiles / rango intercuartílico. La varianza y la desviación estándar están estrechamente relacionados con cada otro- la desviación estándar siempre es igual a la raíz cuadrada de la varianza.
Las fórmulas para la población y la varianza de la muestra son:
Varianza de la población:
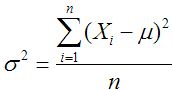
Varianza de la muestra:
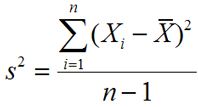
Los percentiles dividir un conjunto de datos en 100 partes iguales cada uno que consiste en un 1 por ciento de los valores en el conjunto de datos. Cuartiles son un tipo especial de percentiles- se separaron los datos en cuatro partes iguales. los intercuartil gama representa el 50 por ciento de la de datos se calcula como el tercer cuartil menos el primer cuartil.
Medidas de asociación
Otro tipo de medida, conocida como medida de asociación, se refiere a relación entre dos muestras o dos poblaciones. Dos ejemplos de ello son la covarianza y el correlación:
Población covarianza:
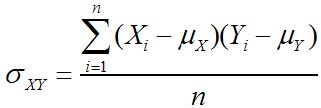
Covarianza de la muestra:
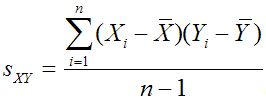
Correlación Población:
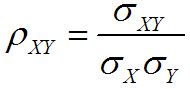
Correlación de la muestra:
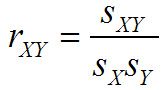
La correlación está estrechamente relacionado con el covariance- se define para asegurar que su valor está siempre entre uno negativo y positivo.
Variables aleatorias y distribuciones de probabilidad en Estadística Empresarial
Variables aleatorias y distribuciones de probabilidad son dos de los conceptos más importantes en las estadísticas. LA variable al azar asigna valores numéricos únicos para los resultados de un experimento- azar este es un proceso que genera resultados inciertos. LA Distribución de probabilidad asigna probabilidades a cada posible valor de una variable aleatoria.
Los dos tipos básicos de las distribuciones de probabilidad son discretas y continuas. Una distribución de probabilidad discreta sólo puede asumir una finito número de valores diferentes.
Ejemplos de distribuciones discretas incluyen:
Binomial
Geométrico
Poisson
Una distribución de probabilidad continua puede asumir una infinito número de valores diferentes. Ejemplos de distribuciones continuas incluyen:
Uniforme
Normalidad
T de Student
Chi-cuadrado
F
Entender muestreo Distribuciones en Estadística Empresarial
En las estadísticas, las distribuciones de muestreo son las distribuciones de probabilidad de cualquier estadística dada en base a una muestra aleatoria, y son importantes porque proporcionan una simplificación importante en la ruta hacia la inferencia estadística. Más específicamente, permiten consideraciones analíticas que se basan en la distribución muestral de un estadístico, más que en la distribución de probabilidad conjunta de todos los valores de las muestras individuales.
Es probable que sea diferente para cada muestra que se extrae de una población El valor de una muestra estadística como la media de la muestra (X). Se puede, por tanto, ser considerado como un variable al azar, cuyas propiedades se pueden describir con una Distribución de probabilidad. La distribución de probabilidad de una muestra estadística se conoce como una distribución muestral.
De acuerdo con un resultado clave en las estadísticas conocidas como el teorema del límite central, la distribución muestral de la media muestral es normal si una de las dos cosas es cierta:
Se necesitan dos momentos para calcular probabilidades para la muestra significado de la media de la distribución muestral es igual a:
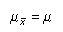
La desviación estándar de la distribución de muestreo (también conocido como el Error estándar) Puede tomar uno de dos valores posibles:
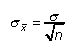
Esta es la elección apropiada para un muestra- "pequeño", por ejemplo, el tamaño de la muestra es menor que o igual a 5 por ciento del tamaño de la población.
Si la muestra es "grande", el error estándar es:
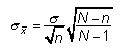
Las probabilidades se pueden calcular para la media de la muestra directamente de la tabla normal estándar mediante la aplicación de la siguiente fórmula:
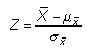
Explora Prueba de hipótesis en Estadística Empresarial
En estadística, hprueba ypothesis se refiere al proceso de elegir entre hipótesis opuestas sobre una distribución de probabilidad, basándose en los datos observados a partir de la distribución. Es un tema central y una parte fundamental del lenguaje de la estadística.
La prueba de hipótesis es un procedimiento de seis pasos:
Hipótesis 1.Null
Hipótesis 2.Alternative
3.Level de significación
Estadística 4.Test
Valor 5.Critical (s)
6.Decision regla
los hipótesis nula es una declaración que se supone que es cierto a menos que haya una fuerte evidencia contradictoria. los hipótesis alternativa es una declaración que será aceptada en lugar de la hipótesis nula si se rechaza.
los nivel de significancia se elige para controlar la probabilidad de un "tipo I" ERROR- este es el error que se produce cuando la hipótesis nula es rechazada erróneamente.
los estadística de prueba y valores críticos se utilizan para determinar si la hipótesis nula debe ser rechazada. los regla de decisión que se sigue es que un resultado estadístico de la prueba "extremas" en el rechazo de la hipótesis nula. Aquí, un estadístico de prueba extrema es aquella que se encuentra fuera de los límites del valor o valores críticos.
Las hipótesis a menudo se prueban sobre los valores de las medidas de la población, como la media y la varianza. También se utilizan para determinar si una población sigue una distribución de probabilidad especificada. También forman una parte importante del análisis de regresión, donde se utilizan hipótesis para validar los resultados de una ecuación de regresión estimada.
Cómo las empresas Estadística Análisis Uso de regresión
El análisis de regresión es una herramienta estadística utilizada para la investigación de las relaciones entre las variables. Por lo general, el investigador desea saber el efecto causal de una variable sobre otra - el efecto de un aumento de precios en la demanda, por ejemplo, o el efecto de los cambios en la oferta monetaria sobre la tasa de inflación.
El análisis de regresión se utiliza para estimar la fuerza y la dirección de la relación entre dos variables linealmente relacionadas: X e Y. X es la variable "independiente" e Y es la variable "dependiente".
Los dos tipos básicos de análisis de regresión son:
El análisis de regresión simple: Se utiliza para estimar la relación entre una variable dependiente y una sola variable independiente, por ejemplo, la relación entre el rendimiento de los cultivos y las precipitaciones.
El análisis de regresión múltiple: Se utiliza para estimar la relación entre una variable dependiente y dos o variables- más independiente, por ejemplo, la relación entre los salarios de los empleados y su experiencia y educación.
El análisis de regresión múltiple introduce varias complejidades adicionales, pero puede producir resultados más realistas que el análisis de regresión simple.
El análisis de regresión se basa en varios supuestos fuertes acerca de las variables que se están estimadas. Varios exámenes claves se utilizan para garantizar que los resultados son válidos, incluyendo pruebas de hipótesis. Estas pruebas se usan para asegurar que los resultados de la regresión no son simplemente debido al azar, pero indican una relación real entre dos o más variables.
Una ecuación de regresión estimada puede utilizarse para una amplia variedad de aplicaciones comerciales, tales como:
Medir el impacto sobre los beneficios de una empresa de un aumento en las ganancias
La comprensión de lo sensible que las ventas de una empresa son a los cambios en los gastos de publicidad
Al ver cómo un precio de las acciones se ve afectado por los cambios en las tasas de interés
El análisis de regresión puede usarse también para pronosticar purposes- por ejemplo, una ecuación de regresión puede usarse para predecir la demanda futura de productos de una empresa.
Debido a la extrema complejidad de los análisis de regresión, que se implementa a menudo mediante el uso de calculadoras especializadas o programas de hojas de cálculo.
3 maneras de describir las poblaciones y muestras en las estadísticas empresariales
Encuentra las pruebas estadísticas apropiadas para dos poblaciones independientes de igual tamaño y varianza
¿Cómo encontrar los momentos de la distribución binomial