Cómo calcular los parámetros y estimadores
En econometría, cuando recoja una muestra aleatoria de los datos y calcular una estadística con esos datos, usted está produciendo una estimación puntual, que es una sola estimación de un parámetro de la población.
Estadísticas descriptivas son medidas que se pueden utilizar para resumir los datos de la muestra y, posteriormente, hacer predicciones sobre su población de interés. Cuando las medidas descriptivas se calculan utilizando datos de población, esos valores se llaman plarámetros. Al calcular medidas descriptivas utilizando datos de la muestra, los valores se llaman estimlares (o estadística).
Se podría estimar muchos parámetros poblacionales con datos de la muestra, pero aquí calcular las estadísticas más populares: media, la varianza, la desviación estándar, la covarianza y correlación. La siguiente lista indica cómo se calcula cada parámetro y su estimador correspondiente.
La media (promedio): los significar es el promedio simple de la variable aleatoria, X. Media de la población de X es
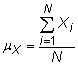
dónde Xyo representa las mediciones individuales y N es el tamaño de la población. La media de la muestra es
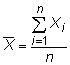
La diferencia entre la muestra y la media poblacional es que que la media de la muestra utiliza el tamaño de la muestra n en lugar del tamaño de la población N.
Varianza: los desacuerdo es el promedio de las diferencias al cuadrado de la media. La varianza de la población de una variable aleatoria X es
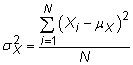
dónde Xyo representa las mediciones individuales,
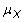
es decir la población, y N es el tamaño de la población. La varianza de la muestra es
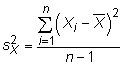
Tenga en cuenta que el denominador de la varianza de la muestra no sólo utiliza el tamaño de la muestra n sino también resta 1 de ese número. Este cambio se conoce como una grados de libertad ajuste. Grados de libertad ajustes suelen ser importante en demostrar que los estimadores son imparciales.
Desviacion estandar: los desviacion estandar medidas de cómo extienden la variable aleatoria es, en promedio, de la media. La desviación estándar es la raíz cuadrada de la varianza, por lo que la desviación estándar de población de variable aleatoria X es
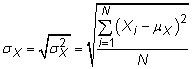
y la desviación estándar de la muestra es
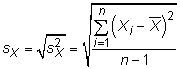
Covarianza: los covarianza mide la cantidad de dos variables aleatorias cambian juntos. La covarianza población entre dos variables aleatorias X y Y es
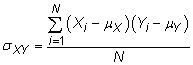
dónde Xyo representa el individuo X valores, Yyo representa el individuo Y valores y N es el número total de mediciones en la población. La covarianza muestral es
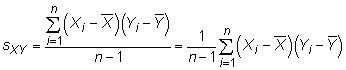
dónde
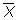
es la media muestral de X,
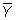
es la media muestral de Y, y n es el tamaño de la muestra.
Correlación: los correlación se refiere a la relación entre dos variables aleatorias o conjuntos de datos. El coeficiente de correlación de la población entre dos variables aleatorias X y Y es
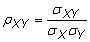
dónde
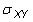
es la covarianza de la población,
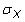
es la desviación estándar de la población de X, y
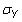
es la desviación estándar de la población de Y. El coeficiente de correlación de la muestra es
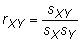
dónde sXY es la covarianza de la muestra, sX es la desviación estándar de la muestra de X, y sY es la desviación estándar de la muestra de Y.
Ahora, trata de trabajar con algunos números. La tabla muestra cinco observaciones de ventas de hamburguesas y precios. Utilice las fórmulas para calcular la media, la varianza, la desviación estándar, la covarianza y correlación.
| Sales de hamburguesas (en unidades), Y | Hamburguesa Precio (en $), X |
|---|---|
| 100 | 1 |
| 80 | 2 |
| 63 | 3 |
| 45 | 4 |
| 21 | 5 |
Usted puede utilizar el software de ordenador, como STATA, para calcular la estadística descriptiva de los datos. Al escribir " suma Nº 148; en la línea de comandos, obtendrá los estadísticos descriptivos de todas las variables en su conjunto de datos. Si desea que la correlación entre dos variables, seleccione Estadísticas-resúmenes, tablas y pruebas-Resumen y estadísticas descriptivas-correlaciones y covarianzas desde la barra de menú.
O bien, puede ingresar " corr variable1 varilable2" en la línea de comandos. En el comando, reemplace variable1 y variable2 con los nombres reales que le has dado las variables en su conjunto de datos. Usted puede obtener covarianza mediante la adición de una opción para el tipo de comandos de correlación " corr varyoable1 variable2, cov " en la línea de comandos.

Debe comprobar que sus cálculos manuales de estas medidas son compatibles con la salida de STATA.
Resumir datos con estadística descriptiva es un procedimiento relativamente sencillo, pero asegúrese de que usted examina cuidadosamente los valores. Usted puede usar medidas descriptivas para asegurar que su muestra contiene medidas que sean realistas. Por ejemplo, si su población de interés es graduados de la universidad, usted no espere que su muestra aleatoria de ese grupo a tener una edad promedio de 21.
Una cuidadosa atención a estos detalles ofrece más credibilidad en los datos y las conclusiones posteriores se realicen.





