Cómo calcular la desviación estándar de un conjunto de datos estadísticos
Con mucho, la medida más común de variación de datos numéricos en las estadísticas es la desviación estándar. los desviacion estandar medidas de cómo los datos son concentran alrededor del significado de la más concentrada, menor es la desviación estándar. No es reportado casi tan a menudo como debería ser, pero cuando es, a menudo se ven entre paréntesis, así: (s = 2.68).
La fórmula para la desviación estándar de la muestra de un conjunto de datos (s) es
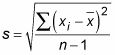
dónde Xyo es cada valor es el conjunto de datos, X-barra es la media, y n es el número de valores en el conjunto de datos. Calcular s, siga los siguientes pasos:
Encuentra la media del conjunto de datos,
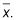
Tome cada valor en el conjunto de datos (X) Y restar la media de ella para llegar
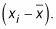
Cuadrados cada una de las diferencias,
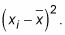
Sume todos los resultados desde el paso 3 para obtener la suma de los cuadrados,
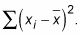
Divida la suma de los cuadrados (que se encuentra en el paso 4) por el número de números en el conjunto de datos, menos de uno, es decir, (n - 1). Ahora tu tienes
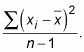
Tome la raíz cuadrada de conseguir
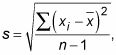
que es la desviación estándar de la muestra, s. ¡Menos mal!
Al final de la Etapa 5 que haya encontrado una estadística llamada varianza de la muestra, denotado por s2. La varianza es otra manera de medir la variación en un ajuste de datos su lado negativo es que es en unidades cuadradas. Si sus datos son en dólares, por ejemplo, la varianza sería en dólares cuadrados - lo que hace no tiene sentido. Es por eso que de continuar con el Paso 6. La desviación estándar tiene las mismas unidades que los datos originales.
Mira el siguiente pequeño ejemplo: Suponga que tiene cuatro puntuaciones de las pruebas: 1, 3, 5 y 7. La media es 16 # 247- 4 = 4 puntos. Restando la media de cada número, se obtiene (1 - 4) = -3, (3 - 4) = -1, (5 - 4) = 1, y (7 - 4) = 3. La cuadratura de cada uno de estos resultados, se obtiene 9, 1, 1 y 9. La adición de estas arriba, la suma es 20. En este ejemplo, n = 4, y por lo tanto n - 1 = 3, por lo que dividir 20 por 3 para obtener 6,67, que es la varianza. Las unidades aquí son " puntos cuadrados, " que obviamente no tiene sentido. Por último, se toma la raíz cuadrada de 6.67, para obtener 2,58. La desviación estándar para estas cuatro puntuaciones de las pruebas es de 2,58 puntos.
Debido a que el cálculo de la desviación estándar implica muchos pasos, en la mayoría de los casos usted tiene una computadora calcular por usted. Sin embargo, saber cómo calcular la desviación estándar ayuda a interpretar mejor esta estadística y puede ayudar a determinar si la estadística puede ser errónea.
-
¿Cuánto propagación es allí en los datos? -
Cómo calcular los parámetros y estimadores -
Aplicando la regla empírica (68-95-99,7) a un conjunto de datos estadísticos -
Los conjuntos de datos y problemas de estadística descriptiva -
Encontrar la desviación estándar de una muestra estadística -
Cómo calcular una correlación
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…
Cómo calcular la varianza y la desviación estándar en la distribución uniforme los distribución uniforme se utiliza para describir una situación en la que todos los posibles resultados de un experimento aleatorio tienen la misma probabilidad de ocurrir. Puede utilizar la varianza y la desviación estándar para medir el…
¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
¿Cómo interpretar la desviación estándar de un conjunto de datos estadísticos La desviación estándar puede ser difícil de interpretar como un solo número por sí solo. Básicamente, una pequeña desviación estándar significa que los valores de un conjunto de datos estadísticos se encuentran cerca de la media del…
¿Cómo medir los momentos de la f-distribución Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…
La desviación estándar y la varianza Los problemas aquí se centran en calcular, interpretar y comparar la desviación estándar y la varianza en las estadísticas básicas. Resuelve los siguientes problemas sobre la desviación estándar y la varianza.Ejemplos de preguntas¿Qué mide…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…
Estadísticas para grandes datos para los maniquíes Medidas de tendencia central muestran el centro de un conjunto de datos. Tres de las medidas más utilizadas de tendencia central son la media, la mediana y la moda.SignificarSignificar es otra palabra para la media. Esta es la fórmula para el…