Cómo calcular una correlación
Can una medida estadística tanto la fuerza y la dirección de una relación lineal entre dos variables? ¡Por supuesto! Los estadísticos utilizan el coeficiente de correlación para medir la fuerza y la dirección de la relación lineal entre dos variables numéricas X y Y. El coeficiente de correlación para una muestra de datos se denota por r.
Aunque la definición de la calle correlación se aplica a cualquiera de los dos elementos que están relacionados (como el género y la afiliación política), los estadísticos utilizan este término sólo en el contexto de dos variables numéricas. El término formal para la correlación es la coeficiente de correlación. Muchos diferentes medidas de correlación se han creado- la utilizada en este caso se denomina Coeficiente de correlación de Pearson.
La fórmula para la correlación (r) es
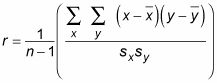
dónde n es el número de pares de datos;
son las medias de las muestras de todos los X-valores y todo el y-valores, respectivamente- y sX y sy son las desviaciones estándar de muestra de todo el X- y y-valores, respectivamente.
Puede utilizar los siguientes pasos para calcular la correlación, r, de un conjunto de datos:
Encuentra la media de todo el X-valores
Encuentra la desviación estándar de todos los X-valores (llamarlo sX) Y la desviación estándar de todos los y-valores (llamarlo sy).
Por ejemplo, para encontrar sX, usted utilizaría la siguiente ecuación:
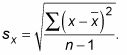
Para cada una de las n pares (X, y) En el conjunto de datos, tomar
Sume el n resultados de la Etapa 3.
Divida la suma por sX # 8727- sy.
Divida el resultado por n - 1, donde n es el número de (X, y) Pares. (Es lo mismo que multiplicar por 1 sobre n - 1.)
Esto le da la correlación, r.
Por ejemplo, suponga que tiene el conjunto de datos (3, 2), (3, 3), y (6, 4). Se calcula el coeficiente de correlación r a través de los siguientes pasos. (Tenga en cuenta que para estos datos el X-valores son 3, 3, 6, y el y-valores son 2, 3, 4.)
El cálculo de la media de los valores x e y, se obtiene
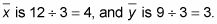
Las desviaciones estándar son sX = 1,73 y sy = 1.00.
los n = 3 diferencias encontradas en el Paso 2 multiplican entre sí son: (3 - 4) (2 - 3) = (- 1) (- 1) = + 1- (3 - 4) (3 - 3) = (- 1) ( 0) = 0- (6 - 4) (4 - 3) = (2) (1) = 2.
Agregar el n = 3 Paso 3 resultados, se obtiene 1 + 0 + 2 = 3.
Dividiendo por sX # 8727- sy le da 3 / (1,73 # 8727- 1,00) = 3 / 1,73 = 1,73. (Es sólo una coincidencia que el resultado del paso 5 es también 1,73.)
Ahora dividir el Paso 5 resultado por 3 - 1 (que es 2), y se obtiene la correlación r = 0.87.
-
Son los elementos del conjunto de datos sin correlación? -
Cómo utilizar la herramienta de análisis de correlación en Excel -
El análisis estadístico con excel para dummies - Cómo calcular las correlaciones de datos en r
- ¿Cómo lidiar con los valores de datos faltantes en r
-
Cómo calcular los parámetros y estimadores
Conexión a la correlación y relaciones lineales Su trabajo aquí es encontrar e interpretar los resultados de una línea de regresión y de sus elementos y comprobar cuidadosamente exactamente lo bien que se adapta a su línea. Nota: Regresión asume que usted ha encontrado que existe una…
Determinar la relación entre variables utilizando covarianza y correlación Usted puede determinar la relación entre dos variables con dos medidas de asociación: Covarianza y correlación. Por ejemplo, si un inversor quiere entender el riesgo de una cartera de acciones, entonces puede utilizar estas medidas para…
Cómo cuadros de correlación, regresión y bidireccionales aclaran datos estadísticos Uno de los objetivos más comunes de la investigación estadística es encontrar vínculos entre las variables. El uso de correlación, regresión y tablas de dos vías, puede utilizar los datos para responder a preguntas como las siguientes:¿Qué…
Cómo covarianza y correlación están relacionados Dos de las medidas más utilizadas de la asociación son covarianza y correlación. Estas medidas están estrechamente relacionados entre otro-, de hecho, se puede pensar de correlación como una versión modificada de la covarianza.La correlación…
Cómo correlación estadística y causalidad son diferentes De todos los temas estadísticos incomprendidos, el que es quizás el más problemático es el mal uso de los conceptos de correlación y causalidad. Correlación, como un término estadístico, es la medida en la que dos variables numéricas tienen…
Cómo calcular una línea de regresión En estadística, se puede calcular una línea de regresión de dos variables si su diagrama de dispersión muestra un patrón lineal y la correlación entre las variables es muy fuerte (por ejemplo, r = 0.98). Una línea de regresión es simplemente…
Cómo interpretar un coeficiente de correlación r En estadística, el coeficiente de correlación r mide la fuerza y la dirección de una relación lineal entre dos variables en un diagrama de dispersión. El valor de r siempre es entre +1 y -1. Para interpretar su valor, ver cuál de los…
¿Cómo se mide la covarianza y correlación de muestras de datos Al comparar las muestras de datos de diferentes poblaciones, dos de las medidas más populares de la asociación son covarianza y correlación. Covarianza y correlación muestran que las variables pueden tener una relación positiva, una relación…
Conocer las condiciones para la regresión Con la regresión lineal simple, usted busca un determinado tipo de relación entre dos variables cuantitativas (numéricas) (como GPA de escuela secundaria y la universidad GPA). Esta relación especial es un relación lineal - uno cuyos pares de…
Medidas de asociación Medidas de asociación cuantificar la fuerza y la dirección de la relación entre dos conjuntos de datos. Estos son los dos más comúnmente utilizados medidas de asociación:CovarianzaCorrelaciónAmbas medidas se utilizan para mostrar cómo…
Estadísticas para grandes datos para los maniquíes Medidas de tendencia central muestran el centro de un conjunto de datos. Tres de las medidas más utilizadas de tendencia central son la media, la mediana y la moda.SignificarSignificar es otra palabra para la media. Esta es la fórmula para el…
La estimación del tamaño de la muestra para pruebas de correlación en bioestadística Para una prueba de correlación en bioestadística (como el de Pearson o el test de Spearman), escoger el gráfico de dispersión que se parece a una cantidad importante de correlación. Cada gráfico muestra el valor de r (el coeficiente de…