Cómo interpretar un coeficiente de correlación r

En estadística, el coeficiente de correlación r mide la fuerza y ​​la dirección de una relación lineal entre dos variables en un diagrama de dispersión. El valor de r siempre es entre +1 y -1. Para interpretar su valor, ver cuál de los siguientes valores de su correlación r es más cercana a:

• Exactamente -1. Una bajada perfecta (negativa) relación lineal

• -0.70. Un descenso fuerte (negativa) relación lineal

• -0.50. Un descenso moderado relación (negativa)

• -0.30. Un descenso débil (negativa) relación lineal

• 0. No hay relación lineal

• +0.30. Un débil subida relación lineal (positiva)

• +0.50. Una relación en subida moderada (positivo)

• +0.70. Una fuerte subida relación lineal (positiva)

• Exactamente 1. Una subida relación lineal perfecta (positivo)

Si el diagrama de dispersión no indica que hay al menos algo de una relación lineal, la correlación no significa mucho. ¿Por qué medir la cantidad de relación lineal si no hay suficiente de uno a hablar de? Sin embargo, usted puede tomar la idea de la relación lineal de dos maneras: 1) Si no hay relación en absoluto existe, el cálculo de la correlación no tiene sentido, porque la correlación sólo se aplica a lineal relaciones- y 2) Si existe una relación fuerte, pero no es lineal, la correlación puede ser engañoso, ya que en algunos casos existe una relación curva fuerte. Es por eso que es crítico para examinar el diagrama de dispersión primero.

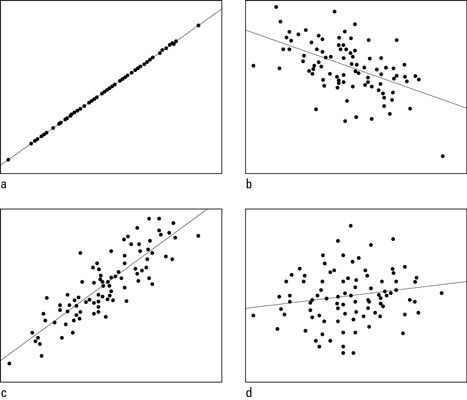
La figura anterior muestra ejemplos de lo que diversas correlaciones parecen, en términos de la fuerza y ​​la dirección de la relación. La figura (a) muestra una correlación de casi 1, la figura (b) muestra una correlación de -0,50, la Figura (c) muestra una correlación de 0,85, y la figura (d) muestra una correlación de 0,15. La comparación de las figuras (a) y (c), que ven la figura (a) es casi una línea recta perfecta en las subidas, y la figura (c) muestran un fuerte patrón lineal cuesta arriba (pero no tan fuerte como la figura (a)). La figura (b) va cuesta abajo pero los puntos son algo dispersa en una banda más ancha, mostrando una relación lineal está presente, pero no tan fuerte como en las figuras (a) y (c). La figura (d) no muestra mucho de nada sucede (y no debería, ya que su correlación es muy cercano a 0).

Muchas personas cometen el error de pensar que una correlación de -1 es una mala cosa, indicando que no hay relación. Todo lo contrario es cierto! Una correlación de -1 significa que los datos se alinean en una línea recta perfecta, la más fuerte relación lineal negativa que puede obtener. los " - " (menos) signo sólo pasa a indicar una relación negativa, una línea de descenso.

¿Qué tan cerca está lo suficientemente cerca de -1 o 1 para indicar una relación lineal suficientemente fuerte? La mayoría de los estadísticos como para ver más allá de las correlaciones al menos 0,5 o -0,5 antes de emocionarse demasiado sobre ellos. No hay que esperar una correlación de estar siempre 0.99 sin embargo- recuerde, estos son los datos reales y los datos reales no son perfectas.