Análisis exploratorio de datos gráfica (eda) técnicas

EDA se basa en gran medida en técnicas gráficas. Puede utilizar técnicas gráficas para identificar las propiedades más importantes de un conjunto de datos. Estas son algunas de las técnicas gráficas más ampliamente utilizados:

• Los diagramas de caja

• Histogramas

• Gráficos de probabilidad normal

• Diagramas de dispersión

Los diagramas de caja

Utiliza diagramas de caja para mostrar algunas de las características más importantes de un conjunto de datos, tales como las siguientes:

• Valor mínimo

• Valor máximo

• Cuartiles

Cuartiles separan un conjunto de datos en cuatro partes iguales. El primer cuartil (Q₁) Es un valor tal que se cumple lo siguiente:

25 por ciento de las observaciones en un conjunto de datos son menores que el primer cuartil.75 por ciento de las observaciones son mayores que el primer cuartil.

El segundo cuartil (Q₂) Es un valor tal que

50 por ciento de las observaciones en un conjunto de datos son menos que el segundo cuartil.50 por ciento de las observaciones son mayores que el segundo cuartil.

El segundo cuartil también se conoce como el mediana.

El tercer cuartil (Q₃) Es un valor tal que

75 por ciento de las observaciones en un conjunto de datos es menor que el tercer cuartil.25 por ciento de las observaciones son mayores que el tercer cuartil.

También puede utilizar diagramas de caja para identificar valores atípicos. Estos son los valores que son sustancialmente diferentes del resto del conjunto de datos. Los valores atípicos pueden causar problemas para las pruebas estadísticas tradicionales, por lo que es importante identificarlos antes de realizar cualquier tipo de análisis estadístico.

Histogramas

Utiliza histogramas para comprender mejor la distribución de probabilidad de que un conjunto de datos sigue. Con un histograma, el conjunto de datos se organiza en una serie de valores individuales o rangos de valores, cada uno representado por una barra vertical. La altura de la barra muestra la frecuencia con que se produce un valor o rango de valores. Con un histograma, es fácil ver cómo se distribuyen los datos.

Diagramas de dispersión

Un diagrama de dispersión es una serie de puntos que muestran cómo dos variables están relacionadas entre sí. Una dispersión aleatoria de puntos indica que las dos variables no están relacionadas, o que la relación entre ellos es muy débil. Si los puntos se parecen mucho a una línea recta, esto indica que la relación entre las dos variables es de aproximadamente lineal.

Dos variables están relacionadas linealmente si se pueden describir con la ecuación Y = mX + b.

X es la variable independiente, y Y es la variable dependiente. m es el cuesta abajo, que representa el cambio en Y debido a un cambio dado en X. b es el interceptar, lo que demuestra el valor de Y cuando X es igual a cero.

La figura muestra un gráfico de dispersión entre dos variables en las que la relación parece ser lineal.

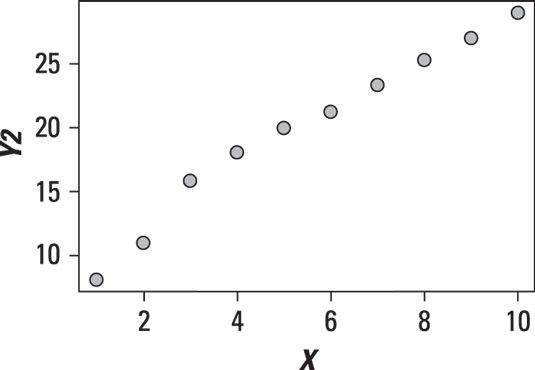
Muy cerca de los puntos en el gráfico de dispersión forman una línea recta. Se inclina un poco hacia la izquierda y se inclina un poco hacia la derecha, pero es más o menos recta. Esto demuestra que la relación es lineal, con una pendiente positiva.

La siguiente figura muestra un gráfico de dispersión entre dos variables en las que Y parece estar aumentando más rápidamente que X.

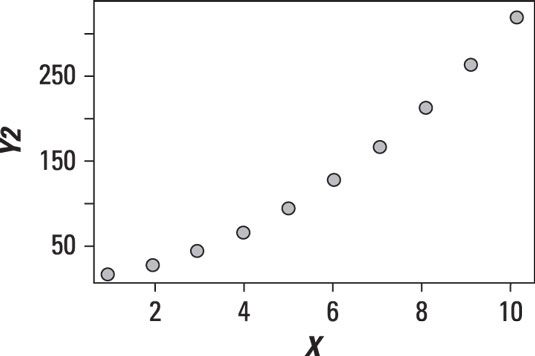
Ver la curva? Esta relación no es claramente lineal. De hecho, es una relación cuadrática. Una relación cuadrática toma la forma Y = aX² + bX + c.

La siguiente figura muestra un gráfico de dispersión en el que no parece haber ninguna relación entre X y Y.

Las variables en el gráfico de dispersión mostradas son no relacionado o independiente- se puede ver esto por la falta de algún patrón en los datos.

Además de mostrar la relación entre dos variables, un gráfico de dispersión también puede mostrar la presencia de valores atípicos. La siguiente figura muestra un conjunto de datos con una observación que es sustancialmente diferente de las otras observaciones.

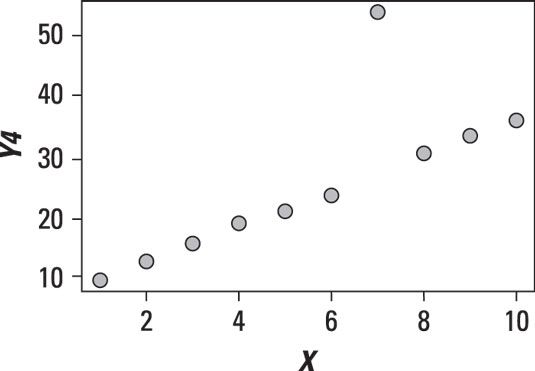
El punto atípico que hay que investigar más para determinar si es el resultado de un error u otros problemas. Es posible que necesitará el valor atípico ser eliminado de los datos.

Gráficos de probabilidad normal

Gráficos de probabilidad normal se utilizan para ver cómo de cerca los elementos de un conjunto de datos siguen la distribución normal. El supuesto de normalidad es común en muchas disciplinas. Por ejemplo, a menudo se asume en finanzas y economía que los rendimientos de las acciones se distribuyen normalmente. El supuesto de normalidad es muy conveniente, y muchas pruebas estadísticas se basan en este supuesto.

La aplicación de las pruebas estadísticas que asumen la normalidad a un no normal conjunto de datos daría resultados muy cuestionables. Por lo tanto, es importante determinar si los datos se distribuyen normalmente antes de realizar cualquiera de estas pruebas estadísticas.