Cuantil-cuantil (qq) parcelas: técnica gráfica de datos estadísticos
LA cuantil-cuantil parcela (también conocido como QQ-plot) Es otra forma se puede determinar si un conjunto de datos coincide con una distribución de probabilidad especificado. QQ-parcelas se utilizan a menudo para determinar si un conjunto de datos es normalmente distribuida. Gráficamente, el QQ-plot es muy diferente de un histograma. Como su nombre indica, se utilizan los ejes horizontal y vertical de un QQ-plot para mostrar cuantiles.
Los cuartiles dividen un conjunto de datos en cuatro grupos iguales, cada uno compuesto de 25 por ciento de los datos. Pero no hay nada particularmente especial sobre el número cuatro. Usted puede elegir cualquier número de grupos que por favor.
Otro tipo popular de cuantil es la percentil, que divide un conjunto de datos en 100 grupos iguales. Por ejemplo, el percentil 30 es el límite entre el 30 por ciento más pequeño de los datos y la mayor 70 por ciento de los datos. La mediana de un conjunto de datos es el percentil 50 del conjunto de datos. El percentil 25 es el primer cuartil y el percentil 75 el tercer cuartil.
Con un QQ-plot, los cuantiles de los datos de la muestra son en el eje vertical, y los cuantiles de una distribución de probabilidad especificada están en el eje horizontal. La trama consiste en una serie de puntos que muestran la relación entre los datos reales y la distribución de probabilidad especificada. Si los elementos de un conjunto de datos se adaptan perfectamente a la distribución de probabilidad especificada, de los puntos de la gráfica formarán una línea de 45 grados.
Por ejemplo, esta cifra muestra un QQ-plot normal para el precio de las acciones de Apple a partir de enero 1, 2013 hasta diciembre 31, 2013.
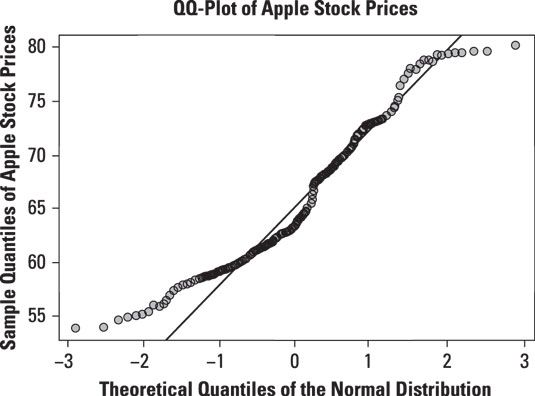
El QQ-gráfico muestra que los precios de las acciones de Apple no se ajustan muy bien a la distribución normal. En particular, la desviación entre precios de las acciones de Apple y la distribución normal parece ser mayor en la parte inferior izquierda; esquina de la gráfica, que corresponde a la cola izquierda de la distribución normal. La discrepancia también es notable en la parte superior derecha; esquina de la gráfica, que corresponde a la cola derecha de la distribución normal.
El gráfico muestra que los más pequeños los precios de las acciones de Apple no son lo suficientemente pequeños para ser coherente con la distribución- normales del mismo modo, los mayores precios de las acciones de Apple no son lo suficientemente grandes como para ser coherente con la distribución normal. Esto demuestra que las colas de la distribución precio de las acciones de Apple son demasiado "delgada" o "flaco" en comparación con la distribución normal. La conclusión que se desprende de esto es que los precios de las acciones de Apple son no normalmente distribuida.
Esta figura muestra un QQ-plot normal para el diario devoluciones de las acciones de Apple de 1 en 2013 hasta 31 dic 2013:
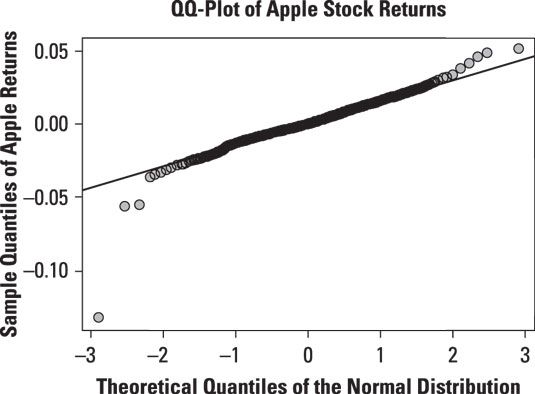
El QQ-plot muestra que los rendimientos de las acciones de Apple no se ajustan a la distribución normal, tampoco. En este caso, el más pequeño vuelve a las acciones de Apple son demasiado pequeños para ser coherente con la distribución normal. Del mismo modo, los mayores vuelve a las acciones de Apple son demasiado grandes para ser coherente con la distribución normal. Esto demuestra que las colas de la distribución de retorno de Apple son demasiado "gruesas" o "grasa" en comparación con la distribución normal. Por lo tanto, las declaraciones de Apple son no normalmente distribuida.
En muchas aplicaciones, se supone que los rendimientos de los activos financieros que se distribuye normalmente, pero en la práctica, estos rendimientos tienden a tener colas "gordos". Con una distribución de cola gorda, extremadamente resultados grandes o pequeños son más frecuentes de lo que haría con la distribución normal. Hay maneras de transformar los datos para ponerlo más en consonancia con la distribución normal.
Distribuciones de probabilidad en el análisis estadístico de datos grande Distribuciones de probabilidad es una de las muchas técnicas estadísticas que pueden ser usados para analizar los datos para encontrar patrones útiles. Se utiliza un Distribución de probabilidad para calcular las probabilidades asociadas…
Cómo utilizar parcelas cuantiles para comprobar la normalidad de datos en r Histogramas dejan mucho a la interpretación del espectador. Una mejor manera gráfica en I de saber si sus datos se distribuyen normalmente es mirar a la llamada cuantil-cuantil (QQ) trama.Con esta técnica, se trazan cuantiles uno contra el otro.…
Econometría y la distribución t los t distribución se utiliza bastante en la econometría. Usted probablemente utilizado el t distribución ampliamente cuando se trata de medios en su clase de estadísticas, pero en la econometría también utilizarlo para coeficientes de…
Poniendo las variables en la misma escala: la distribución normal estándar (z) En econometría, una versión específica de una variable aleatoria normalmente distribuida es la normal estándar. LA distribución normal estándar es una distribución normal con una media de 0 y una varianza de 1. Es útil porque se puede…
Reconociendo las variables habituales: distribución normal En econometría, una variable aleatoria con una distribución normal tiene una función de densidad de probabilidad de que es continsuperfluo, simétrico, y encampanado. Aunque muchas variables aleatorias pueden tener una distribución en forma de…
Estadísticas de las empresas: rendimientos de los activos de modelado con distribución normal Mparticipantes ercado - analistas de renta variable, los gestores de riesgos, los gestores de carteras, los comerciantes y los economistas - deben ser capaces de medir con precisión y modelar el riesgo y el rendimiento de los activos financieros.…
Distribuciones de probabilidad discretas y continuas Los dos tipos básicos de las distribuciones de probabilidad se conocen como discreta y continua. Discreta distribuciones describen las propiedades de una variable al azar para los que se asigna cada resultado individual una probabilidad…
¿Cómo se ve afectada una distribución de muestreo cuando la distribución no es normal En estadística, si una población X tiene cualquier distribución que es no lo normal, o si su distribución es desconocida, no se puede decir de forma automática la distribución de las medias de la muestratiene una distribución normal. Pero…
Cómo el número de grados de libertad afecta a la gráfica de una distribución t Una de las propiedades interesantes de la distribución t es que cuanto mayor es el grado de libertad, más de cerca la distribución t se asemeja a la distribución normal estándar. A medida que los grados de libertad aumenta, el área en las…
¿Cómo encontrar percentiles de una distribución t Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…