Pruebas gráficas de los valores extremos de datos

La identificación de los valores atípicos de datos no es una cuestión de corte y secado. No puede haber desacuerdo sobre lo que hace y no califica como un valor atípico. La definición de un valor atípico depende de la distribución de probabilidad asumida de una población. Por ejemplo, si la población realmente tiene una distribución normal, la gráfica de un conjunto de datos debe tener la misma forma de la firma de campana - si no es así, eso podría ser una señal de que hay valores atípicos en los datos.

Usted puede usar tres técnicas gráficas para identificar valores atípicos:

• Histogramas

• Los diagramas de caja

• QQ-parcelas

Histogramas

LA histograma es un gráfico utilizado para representar visualmente una distribución de probabilidad con una serie de barras verticales. El eje horizontal muestra los valores o rangos de valores para la variable que se está estudiando, y el eje vertical muestra las frecuencias correspondientes de estos valores.

A modo de ejemplo, el Standard and Poors 500 índice (SP 500) es un índice bursátil que representa el precio de las 500 mayores acciones de Estados Unidos, ponderados por su capitalización de mercado. De una acción capitalización de mercado es igual al precio por veces comparten el número de acciones en circulación.

La figura muestra un histograma de los retornos diarios de 500 valores de índice de mercado de la Standard and Poor durante los años 2009-2013.

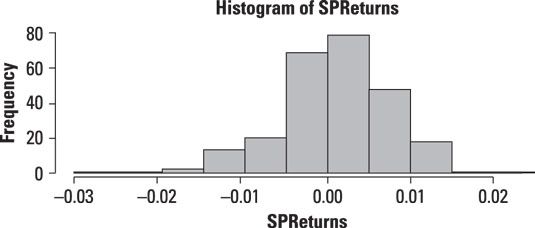
De acuerdo con este histograma, la mayoría de los rendimientos eran cerca de cero durante este período. Devoluciones anteriores 0,01 (1 por ciento) o por debajo de -0,01 (-1 por ciento) ocurrieron con poca frecuencia. Sin embargo, para las declaraciones de que no se producen fuera de la gama pequeña alrededor de 0, la aparición de rendimientos negativos superado la aparición de rendimientos positivos, como se ve por la extrema longitud de la cola izquierda.

La forma del histograma muestra que es poco probable que sea normal, la distribución de los rendimientos en el Standard and Poor 500 durante este período. Un problema es que la distribución normal es simétrica alrededor de su media, mientras que el histograma muestra que la distribución de los rendimientos es sesgado negativamente (es decir, hay un desequilibrio entre los rendimientos negativos y positivos, con más negativo que rentabilidades positivas).

Los diagramas de caja

LA diagrama de caja muestra la distribución de un conjunto de datos en una caja. El cuadro se basa en cuartiles, que son como los percentiles excepto que sólo cuatro de ellos son. El diagrama de caja se estructura de la siguiente manera:

• La parte superior del cuadro representa la tercer cuartil (o cuartil superior) (Q₃) De los datos. Esto es equivalente al 75 por ciento.

• La parte inferior de la caja representa la primer cuartil (o cuartil inferior) (Q₁) De los datos. Esto es equivalente al percentil 25a.

• El centro de la caja (que se muestra con una línea) representa la segundo cuartil (Q₂) De los datos (también conocidas como la mediana).

El primer cuartil de un conjunto de datos es un valor que es mayor que 25 por ciento de los elementos del conjunto de datos y menor que el 75 por ciento restante. El segundo cuartil (es decir, la mediana) es un valor que es mayor que 50 por ciento de los elementos y menor que el 50 por ciento restante. El tercer cuartil es un valor que es mayor que 75 por ciento de los elementos y menor que el 25 por ciento restante.

los rango intercuartil (IQR) se define como la diferencia entre el tercer y primer cuartil:

IQR = Q₃ - Q₁

los IQR se utiliza como una medida de dispersión, o cómo difundir los datos están alrededor del centro. También se puede utilizar para identificar valores atípicos.

Para un diagrama de caja, hay líneas arriba y abajo de la caja. La línea superior representa el valor máximo de un conjunto de datos, con exclusión de los valores atípicos. La línea inferior representa el valor mínimo de un conjunto de datos, excluyendo de nuevo los valores atípicos. Los puntos individuales se muestran arriba y por debajo de estas líneas son los valores extremos del conjunto de datos.

Cuando usted está usando un diagrama de caja, un valor atípico se define de la siguiente manera:

• Si un punto de datos está por debajo de Q₁ - 1.5 (RIC), que es considerado como una de las demás.

• Si un punto de datos está por encima de Q₃ + 1.5 (RIC), que es considerado como una de las demás.

La siguiente figura muestra un diagrama de caja de los diarios vuelve al índice bursátil S & P 500 durante los años 2009-2013.

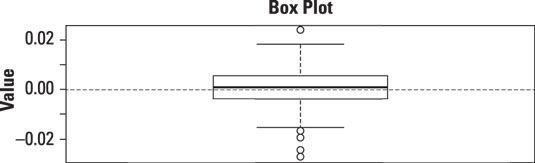
El diagrama de caja muestra que hay un valor atípico que es significativamente mayor que el resto de los retornos en el conjunto de datos. También hay cuatro valores atípicos que son significativamente más pequeño que el resto de los retornos en el conjunto de datos. La existencia de estos valores extremos muestra que el conjunto de datos no puede ser distribuida normalmente.

QQ-parcelas

Puede representar datos de la muestra con un QQ-plot (abreviatura de cuantil-cuantil parcela). Esta parcela se comparan los cuantiles de los datos de la muestra con los cuantiles de una distribución de probabilidad especificada, como la normal.

Cuantiles se utilizan para dividir un conjunto de datos en grupos de igual tamaño en función del valor de una variable numérica particular. Hay varios tipos de cuantiles, incluyendo las siguientes:

• Los percentiles dividir un conjunto de datos en 100 grupos iguales, cada uno correspondiente a un porcentaje del total. Por ejemplo, si un grupo de 1.000 estudiantes toma un examen estandarizado, y 200 de ellos reciben una puntuación por debajo de 300, luego 300 sería el percentil 20 de este conjunto de datos. Esto indica que el 20 por ciento de los estudiantes obtuvo calificaciones por debajo de 300, mientras que el 80 por ciento restante anotó superior a 300.

• Deciles dividir un conjunto de datos en diez grupos iguales, representando cada uno el 10 por ciento del total. Por ejemplo, el cuarto decil corresponde al percentil 40a.

• Cuartiles dividir un conjunto de datos en cuatro grupos iguales, cada uno representando 25 por ciento del total. Por ejemplo, el tercero cuartil corresponde al percentil 75.

La siguiente figura muestra un QQ-plot de los diarios vuelve al SP 500 valores de índice de mercado durante desde 2009 hasta 2013, en comparación con la distribución normal:

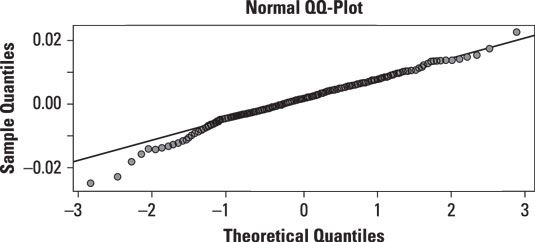
La línea continua en el gráfico representa los cuantiles de la distribución normal. 0 representa el significado, por lo tanto, la mitad de los valores están por debajo de 0, y son un medio por encima de ella. Alrededor del 95 por ciento de los valores están por debajo de 2 (2 representa dos desviaciones estándar por encima de la media), mientras que el 5 por ciento de los valores están por debajo de -2 (-2 representa dos desviaciones estándar por debajo de la media). Si se distribuyen normalmente los rendimientos SP, sus cuantiles deben estar en la línea.

Los puntos de la gráfica son las observaciones reales en el conjunto de datos SP 500. Para los cuantiles normales que son mayores que 2 (es decir, dos desviaciones estándar por encima de la media), el SP 500 retornos están por encima de la línea, lo que indica que la cola derecha es demasiado "gorda" para ser coherente con la distribución normal. Para cuantiles normales que están por debajo de -1 (es decir, una desviación estándar por debajo de la media), el SP 500 retornos debajo de la línea, lo que indica que la cola izquierda también es demasiado gordo para ser coherente con la distribución normal.

En general, la distribución de vuelve a la SP 500 parece ser una distribución de grasa de cola, lo que significa que los resultados extremos son mucho más probable que lo que sería el caso con la distribución normal.