Parcelas de autocorrelación: técnica gráfica de datos estadísticos
Un autocorrelación trama muestra las propiedades de un tipo de datos conocidos como una serie de tiempo. LA series de tiempo se refiere a las observaciones de una sola variable en un horizonte de tiempo determinado. Por ejemplo, el precio diario de acciones de Microsoft durante el año 2013 es una serie de tiempo.
Los datos de la sección transversal se refiere a las observaciones de muchas variables en un solo punto en el tiempo. Por ejemplo, los precios de cierre de las 30 acciones contenidas en el Dow Jones de Industriales, el 31 de enero de 2014, se considerarían datos transversales.
Una parcela de autocorrelación está diseñado para demostrar si los elementos de una serie de tiempo se correlacionan positivamente, negativamente correlacionada o independientes entre sí. (El prefijo auto significa "yo" - autocorrelación se refiere específicamente a la correlación entre los elementos de una serie de tiempo).
Una parcela de autocorrelación muestra el valor de la función de autocorrelación (ACF) en el eje vertical. Puede variar desde -1 a 1.
El eje horizontal de un gráfico de autocorrelación muestra el tamaño de la retraso entre los elementos de la serie temporal. Por ejemplo, la autocorrelación con lag 2 es la correlación entre los elementos de series de tiempo y los elementos correspondientes que se observaron dos períodos de tiempo antes.
Esta cifra muestra un gráfico de autocorrelación de los precios diarios de las acciones de Apple desde enero 1ro, 2013 hasta diciembre 31, 2013.
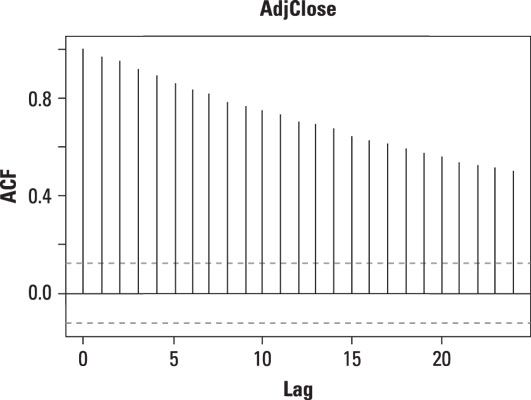
En el gráfico, hay una línea vertical (un "pico") correspondiente a cada lag. La altura de cada pico muestra el valor de la función de autocorrelación para el retraso.
La autocorrelación con cero lag siempre es igual a 1, ya que esto representa la autocorrelación entre cada término y en sí. Precio y precio con retardo cero son la misma variable.
Cada pico que se eleva por encima o cae por debajo de las líneas de trazos se considera que es Estadísticamente significante. (Capítulo 16 habla de esto en detalle.) Esto significa que el pico tiene un valor que es significativamente diferente de cero. Si un pico es significativamente diferente de cero, es evidencia de autocorrelación. Un pico que está cerca de cero es evidencia en contra de autocorrelación.
En este ejemplo, las espigas son estadísticamente significativas para retrasos de hasta 24. Esto significa que los precios de las acciones de Apple están altamente correlacionados entre sí. En otras palabras, cuando el precio de las acciones de Apple se eleva, tiende a seguir subiendo. Cuando el precio de las acciones de Apple cae, tiende a seguir cayendo. Esta figura ilustra esto.
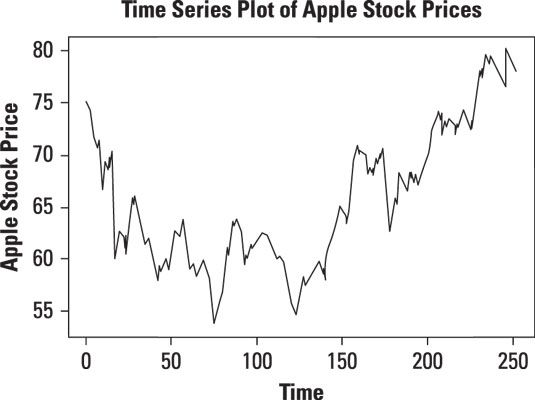
A pesar de que los precios diarios de las acciones de Apple están altamente correlacionados, los rendimientos diarios no pueden ser. A calcular los retornos diarios de los precios diarios de la siguiente manera:
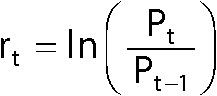
dónde
rt = El retorno compuesto continuo en el tiempo tPt = El precio en el tiempo tPt-1 = El precio en el tiempo t - 1 (un período anterior t)ln = logaritmo natural
El logaritmo natural es el logaritmo con la base e, que es aproximadamente igual a 2,71828 # 133-.
Esta cifra muestra un gráfico de autocorrelación para los diarios regresa a las acciones de Apple a partir de 1 de enero 2013 al 31 de diciembre de 2013.
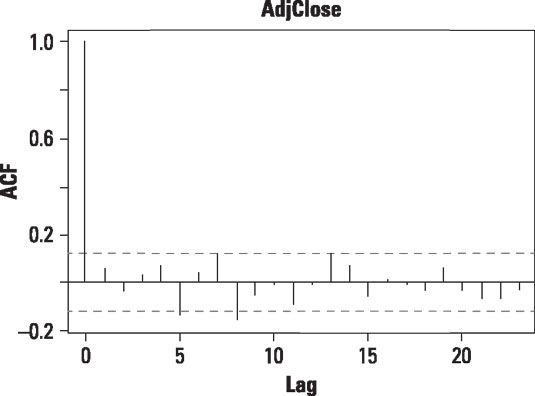
La trama de autocorrelación para retornos diarios a las acciones de Apple demuestra que la mayoría de los picos no son estadísticamente significativas. Esto indica que los rendimientos no están altamente correlacionados, como se muestra.
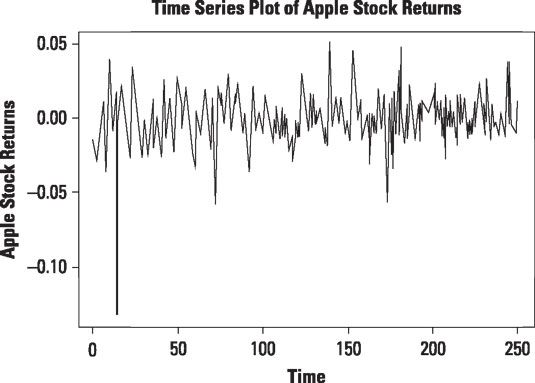
El gráfico muestra que a excepción de una crisis mayor, la rentabilidad de las acciones de Apple entre enero 1 de 2013 y 31 de diciembre 2013 no muestran ningún patrón particular - que tienden a fluctuar al azar alrededor de cero. Esto significa que los rendimientos son en gran parte independientes entre sí.
Puede utilizar una parcela de autocorrelación para determinar si los elementos de una serie de tiempo son aleatorio (es decir, sin relación entre sí). Esto es importante, porque muchas pruebas estadísticas que involucran series de tiempo se basan en este supuesto.
Como se puede ver, hay muchas maneras diferentes para visualizar sus datos. Una imagen vale más que mil palabras, como dice el refrán. Y sin duda es cierto en el análisis de datos. Paquetes de software estadísticos generalmente vienen equipados con herramientas gráficas fáciles de usar. Al tomar ventaja de ellos, puede obtener rápidamente una idea de sus datos que ninguna cantidad de cálculos numéricos que podría dar.
-
Son los elementos del conjunto de datos sin correlación? -
Los diagramas de caja: técnica gráfica de datos estadísticos -
¿El centro o propagación de un cambio de conjunto de datos a través del tiempo? -
Técnicas Eda para supuestos de prueba -
Pruebas gráficas de los valores extremos de datos -
Histogramas: técnica gráfica de datos estadísticos
¿Cuánto propagación es allí en los datos? Cuando se trabaja con estadísticas de datos grandes, se identifica la difusión de un conjunto de datos del centro con varias diferentes medidas de resumen: varianza, desviación estándar, cuartiles, rango intercuartil (IQR).La varianza es la…
Cuantil-cuantil (qq) parcelas: técnica gráfica de datos estadísticos LA cuantil-cuantil parcela (también conocido como QQ-plot) Es otra forma se puede determinar si un conjunto de datos coincide con una distribución de probabilidad especificado. QQ-parcelas se utilizan a menudo para determinar si un conjunto de…
Gráficos de dispersión: técnica gráfica de datos estadísticos A diferencia de un diagrama de tallo y hojas, un gráfico de dispersión está destinado a mostrar la relación entre de dos variables. Puede ser difícil de ver si hay una relación entre dos variables con sólo mirar los datos en bruto, pero con…
Diagramas de tallo y hojas: técnica gráfica de datos estadísticos LA tallo y hoja trama es un dispositivo gráfico en el que la distribución de un conjunto de datos está organizada por el valor numérico de las observaciones en el conjunto de datos. El diagrama consiste en una "madre", que muestra las diferentes…
Una inspección gráfica de los residuos Correlación serial en el término de error (autocorrelación) es un problema común para la estimación de regresión OLS, especialmente con series de tiempo y datos de panel. Sin embargo, por lo general, no tiene manera de saber con antelación si…
Estimación econométrica y los supuestos CLRM Técnicas econométricas se utilizan para estimar los modelos económicos, que en última instancia le permiten explicar cómo varios factores afectan a algunos resultados de interés o para pronosticar eventos futuros. La técnica de mínimos…
Intercepta y / o pendientes que cambian con el tiempo A diferencia del análisis de sección transversal típica, que impone una naturaleza estática de sus modelos, una sección transversal combinado le permite incorporar un elemento de tiempo dinámico. Usted puede hacer esto con una sección…
Los patrones de autocorrelación LAutocorrelation, también conocido como correlación serial, pueden existir en un modelo de regresión cuando la orden de las observaciones en los datos es relevante o importante. En otras palabras, con series de tiempo (ya veces panel o…
Estadísticas de las empresas: utilizan el análisis de regresión para determinar la validez de las relaciones El análisis de regresión es una de las técnicas estadísticas más importantes para aplicaciones de negocios. Es una metodología estadística que ayuda a estimar la fuerza y la dirección de la relación entre dos o más variables. El…
Cómo estimar una tendencia en un modelo de regresión de series de tiempo Para estimar un modelo de regresión de series de tiempo, una tendencia debe ser estimado. Se empieza por la creación de un gráfico de líneas de las series temporales. El gráfico de líneas muestra cómo una variable cambia con el tiempo- que…
Cómo mostrar la relación entre dos variables utilizando un gráfico de dispersión LA gráfico de dispersión (también conocido como diagrama de dispersión) Muestra la relación entre dos variables cuantitativas) (numéricos. Estas variables pueden estar relacionadas positivamente, negativamente relacionada o no…
Información general de las técnicas gráficas Existen diferentes tipos de gráficos pueden ser útiles para el análisis de datos. Estos incluyen diagramas de tallo y hojas, gráficos de dispersión, diagramas de caja, histogramas, cuantil-cuantil (QQ) parcelas y parcelas de autocorrelación.LA…