Son los elementos del conjunto de datos sin correlación?
Para un conjunto de datos que consiste en observaciones tomadas en diferentes puntos en el tiempo (es decir, datos de series de tiempo), Es importante para determinar si o no las observaciones están correlacionadas entre sí. Esto es porque muchas técnicas para el modelado de datos de series de tiempo se basan en la suposición de que los datos no está correlacionado entre sí (independiente).
Una técnica gráfica que puede utilizar para ver si los datos no está correlacionado con los demás es la función de autocorrelación. La función de autocorrelación muestra la correlación entre las observaciones en una serie de tiempo con diferentes rezagos. Por ejemplo, la correlación entre las observaciones con retardo 1 se refiere a la correlación entre cada observación individual y su valor anterior.
Esta figura muestra la función de autocorrelación de los retornos diarios de ExxonMobil en 2013.
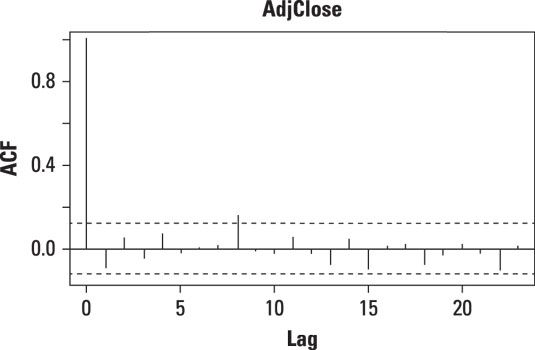
Cada "pico" en la función de autocorrelación representa la correlación entre las observaciones con un desfase dado.
La autocorrelación con un desfase 0 siempre es igual a 1, ya que este representa las correlaciones de las observaciones con ellos mismos.
En el gráfico, las líneas discontinuas representan los límites inferior y superior de una intervalo de confianza. Si un pico se eleva por encima del límite superior del intervalo de confianza o cae por debajo del límite inferior del intervalo de confianza, que muestra que la correlación para ese retraso no es 0. Esto es evidencia en contra de la independencia de los elementos de un conjunto de datos.
En este caso, sólo hay un pico estadísticamente significativa (al lag 8). Este pico muestra que los rendimientos de ExxonMobil pueden ser independientes. Una prueba estadística más formal podría mostrar si eso es cierto o no.
-
Parcelas de autocorrelación: técnica gráfica de datos estadísticos -
Los diagramas de caja: técnica gráfica de datos estadísticos -
¿El centro o propagación de un cambio de conjunto de datos a través del tiempo? -
Técnicas Eda para supuestos de prueba -
Análisis exploratorio de datos gráfica (eda) técnicas -
Pruebas gráficas de los valores extremos de datos
¿Cuánto propagación es allí en los datos? Cuando se trabaja con estadísticas de datos grandes, se identifica la difusión de un conjunto de datos del centro con varias diferentes medidas de resumen: varianza, desviación estándar, cuartiles, rango intercuartil (IQR).La varianza es la…
Cómo nuevas predicciones analíticas con regresión r Para hacer predicciones analíticas con nuevos datos, sólo tiene que utilizar la función con una lista de los siete valores de los atributos. El siguiente código hace ese trabajo:> NewPrediction lt; - predecir (modelo,
lista (cilindros =…
Diagramas de tallo y hojas: técnica gráfica de datos estadísticos LA tallo y hoja trama es un dispositivo gráfico en el que la distribución de un conjunto de datos está organizada por el valor numérico de las observaciones en el conjunto de datos. El diagrama consiste en una "madre", que muestra las diferentes…
El análisis estadístico con excel para dummies Excel puede ayudarle a hacer todo tipo de cálculos. He aquí una selección de funciones de hoja de estadísticas de Excel. Cada uno de ellos devuelve un valor en una celda seleccionada.Tendencia central y variabilidadFunciónLo que…
Cómo calcular las correlaciones de datos en r La cantidad en la que dos variables de datos varían juntos puede ser descrita por el coeficiente de correlación. En R, se obtiene la correlación entre un conjunto de variables muy fácilmente mediante el uso de la cor () función. Sólo tiene que…
¿Cómo lidiar con los valores de datos faltantes en r los cor () función en R puede lidiar con la falta de valores de datos de múltiples maneras. Para ello, establece el argumento usar a uno de los posibles valores de texto. El valor de la usar argumento es especialmente importante si usted calcula…
Observaciones de nomenclatura en r Una diferencia importante entre una matriz y una trama de datos en R es que las tramas de datos siempre han llamado observaciones. Mientras que el rownames () retornos de función NULO si no especificó los nombres de las filas de una matriz,…
Una inspección gráfica de los residuos Correlación serial en el término de error (autocorrelación) es un problema común para la estimación de regresión OLS, especialmente con series de tiempo y datos de panel. Sin embargo, por lo general, no tiene manera de saber con antelación si…
Los patrones de autocorrelación LAutocorrelation, también conocido como correlación serial, pueden existir en un modelo de regresión cuando la orden de las observaciones en los datos es relevante o importante. En otras palabras, con series de tiempo (ya veces panel o…
Cómo calcular una correlación Can una medida estadística tanto la fuerza y la dirección de una relación lineal entre dos variables? ¡Por supuesto! Los estadísticos utilizan el coeficiente de correlación para medir la fuerza y la dirección de la relación…
Cómo interpretar un coeficiente de correlación r En estadística, el coeficiente de correlación r mide la fuerza y la dirección de una relación lineal entre dos variables en un diagrama de dispersión. El valor de r siempre es entre +1 y -1. Para interpretar su valor, ver cuál de los…
Medidas de asociación Medidas de asociación cuantificar la fuerza y la dirección de la relación entre dos conjuntos de datos. Estos son los dos más comúnmente utilizados medidas de asociación:CovarianzaCorrelaciónAmbas medidas se utilizan para mostrar cómo…