¿El centro o propagación de un cambio de conjunto de datos a través del tiempo?
Para los datos de series de tiempo, es importante saber si las observaciones siguen teniendo la misma media en el tiempo y si la varianza de los datos está cambiando con el tiempo.
Muchas pruebas estadísticas y técnicas de pronóstico dependen de este supuesto.
La figura muestra una serie parcela momento de los retornos diarios de ExxonMobil en todo 2013.
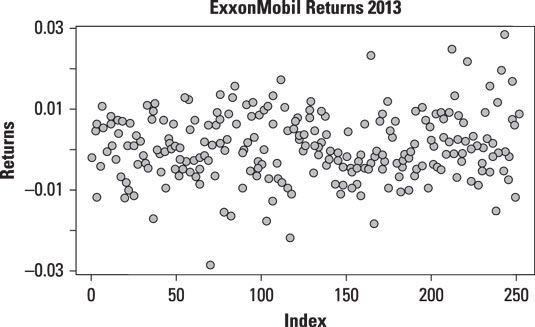
El gráfico muestra que a medida que transcurre el tiempo, las observaciones parecen estar centrado en torno a cero. Esto indica que la media no está cambiando con el tiempo. Si la media fueron aumentando con el tiempo, los puntos de la gráfica tenderían a desplazarse arriba si la media fueron cayendo con el tiempo, los puntos de la gráfica tenderían a desplazarse hacia abajo.
Para los datos de series de tiempo, también es importante saber si la varianza de los datos está cambiando con el tiempo. La figura muestra que a medida que pasa el tiempo, el diferencial entre las observaciones está creciendo constantemente. (Es decir, los datos es cada vez más extendido como el tiempo transcurrido.) Esto indica que la varianza (así como la desviación estándar) está aumentando con el tiempo.
Si la varianza está cambiando con el tiempo, que puede causar serios problemas a muchas técnicas estadísticas. Afortunadamente, hay métodos disponibles que pueden corregir este problema.
La situación en la varianza no es constante en el tiempo tiene un nombre muy intimidante en la econometría: heteroscedasticidad. Pronunciando esta palabra no es fácil!
-
Son los elementos del conjunto de datos sin correlación? -
Parcelas de autocorrelación: técnica gráfica de datos estadísticos -
Los diagramas de caja: técnica gráfica de datos estadísticos -
Técnicas Eda para supuestos de prueba -
Análisis exploratorio de datos gráfica (eda) técnicas -
Histogramas: técnica gráfica de datos estadísticos
¿Cuánto propagación es allí en los datos? Cuando se trabaja con estadísticas de datos grandes, se identifica la difusión de un conjunto de datos del centro con varias diferentes medidas de resumen: varianza, desviación estándar, cuartiles, rango intercuartil (IQR).La varianza es la…
El análisis estadístico con excel para dummies Excel puede ayudarle a hacer todo tipo de cálculos. He aquí una selección de funciones de hoja de estadísticas de Excel. Cada uno de ellos devuelve un valor en una celda seleccionada.Tendencia central y variabilidadFunciónLo que…
Cómo calcular los parámetros y estimadores En econometría, cuando recoja una muestra aleatoria de los datos y calcular una estadística con esos datos, usted está produciendo una estimación puntual, que es una sola estimación de un parámetro de la población.Estadísticas descriptivas…
¿Cómo distinguir entre perturbaciones homocedástico y heteroscedásticos El término de error es el componente más importante del modelo de regresión lineal clásica (CLRM). La mayor parte de los supuestos que permiten econometristas CLRM para probar las propiedades deseables de los estimadores MCO (el teorema de…
La distribución chi-cuadrado en la econometría En econometría, se utiliza la distribución chi-cuadrado ampliamente. La distribución chi-cuadrado es útil para comparar los valores de varianza estimada de una muestra a esos valores basados en supuestos teóricos. Por lo tanto, se utiliza…
3 maneras de describir las poblaciones y muestras en las estadísticas empresariales Cuando se trabaja con las poblaciones y muestras (un subconjunto de una población) en estadísticas de las empresas, puede utilizar tres tipos comunes de medidas para describir el conjunto de datos: tendencia central, dispersión y asociación.Por…
Cómo calcular la desviación estándar de un conjunto de datos estadísticos Con mucho, la medida más común de variación de datos numéricos en las estadísticas es la desviación estándar. los desviacion estandar medidas de cómo los datos son concentran alrededor del significado de la más concentrada, menor es la…
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…
La desviación estándar y la varianza Los problemas aquí se centran en calcular, interpretar y comparar la desviación estándar y la varianza en las estadísticas básicas. Resuelve los siguientes problemas sobre la desviación estándar y la varianza.Ejemplos de preguntas¿Qué mide…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…