3 maneras de describir las poblaciones y muestras en las estadísticas empresariales

Cuando se trabaja con las poblaciones y muestras (un subconjunto de una población) en estadísticas de las empresas, puede utilizar tres tipos comunes de medidas para describir el conjunto de datos: tendencia central, dispersión y asociación.

Por convención, las fórmulas estadísticas que se utilizan para describir las medidas de población contienen letras griegas, mientras que las fórmulas utilizadas para describir las medidas de ejemplo contienen letras latinas.

Medidas de tendencia central

En estadística, la media, la mediana y la moda son conocidos como medidas de tendencia central- que se utilizan para identificar el centro de un conjunto de datos:

• La media de: El valor entre los valores mayor y menor de un conjunto de datos, que se obtiene por un método prescrito.

• Mediana: El valor que divide un conjunto de datos en dos mitades iguales

• Modo: El valor más comúnmente observada en un conjunto de datos

Las muestras se eligen al azar a partir de poblaciones. Si este proceso se lleva a cabo correctamente, cada muestra debe reflejar con precisión las características de la población. Por lo tanto, una medida de la muestra, tales como el significa, debe ser una buena estimación de la medida de población correspondiente. Considere los siguientes ejemplos de media:

Media de la población:

Esta fórmula simplemente le dice al sumar todos los elementos de la población y se dividen por el tamaño de la población.

Media de la muestra:

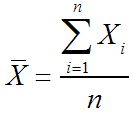
El proceso para calcular esto es exactamente el mismo: se suman todos los elementos de la muestra y se dividen por el tamaño de la muestra.

Además de las medidas de tendencia central, otros dos tipos principales de medidas son medidas de dispersión (spread) y medidas de asociación.

Medidas de dispersión

Medidas de dispersión incluir varianza / desviación estándar y percentiles / cuartiles / rango intercuartílico. La varianza y la desviación estándar están estrechamente relacionados con cada otro- la desviación estándar siempre es igual a la raíz cuadrada de la varianza.

Las fórmulas para la población y la varianza de la muestra son:

Varianza de la población:

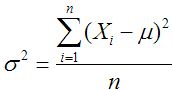
Varianza de la muestra:

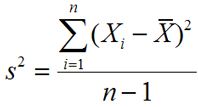
Los percentiles dividir un conjunto de datos en 100 partes iguales cada uno que consiste en un 1 por ciento de los valores en el conjunto de datos. Cuartiles son un tipo especial de percentiles- se separaron los datos en cuatro partes iguales. los intercuartil gama representa el 50 por ciento de la de datos se calcula como el tercer cuartil menos el primer cuartil.

Medidas de asociación

Otro tipo de medida, conocida como medida de asociación, se refiere a relación entre dos muestras o dos poblaciones. Dos ejemplos de ello son la covarianza y el correlación:

Población covarianza:

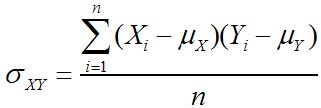
Covarianza de la muestra:

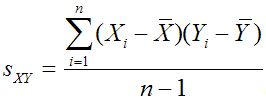
Correlación Población:

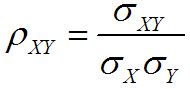
Correlación de la muestra:

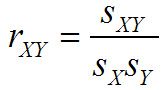
La correlación está estrechamente relacionado con el covariance- se define para asegurar que su valor está siempre entre uno negativo y positivo.