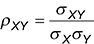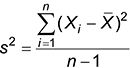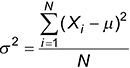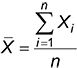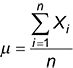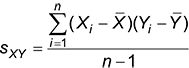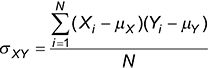Medidas de tendencia central muestran el centro de un conjunto de datos. Tres de las medidas más utilizadas de tendencia central son la media, la mediana y la moda.
Significar
Significar es otra palabra para la media. Esta es la fórmula para el cálculo de la media de una muestra:
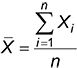
Con esta fórmula, calcular la media de la muestra simplemente sumando todos los elementos de la muestra y dividiendo por el número de elementos en la muestra.
Aquí está la fórmula correspondiente para el cálculo de la media de una población:
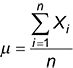
Aunque la notación es ligeramente diferente, el procedimiento para calcular una media poblacional es el mismo que el procedimiento para calcular una media de la muestra.
Letras griegas se utilizan para describir las poblaciones, mientras que las letras romanas se utilizan para describir las muestras.
La mediana
los mediana de un conjunto de datos es un valor que divide los datos en dos mitades iguales. En otras palabras, la mitad de los elementos de un conjunto de datos se menos que la mediana y la otra mitad son mas grande que la mediana. El procedimiento para el cálculo de la mediana es la misma para ambas muestras y poblaciones.
Modo
El modo de un conjunto de datos es el valor más comúnmente observado en el conjunto de datos. Usted determina el modo de la misma manera para una muestra y una población.
Medidas de dispersión central
Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:
Rango
Varianza
Desviacion estandar
Rango
los alcance de un conjunto de datos es la diferencia entre el valor mayor y el menor valor. A calcular de la misma manera para ambas muestras y poblaciones.
Varianza
Usted puede pensar en la varianza como el promedio cuadrado diferencia entre los elementos de un conjunto de datos y la media. Las fórmulas para calcular una varianza de la muestra y una varianza de la población son ligeramente diferentes.
Aquí está la fórmula para el cálculo de la varianza de la muestra:
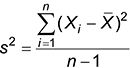
Y aquí está la fórmula para el cálculo de varianza de la población:
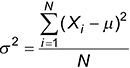
Desviacion estandar
La desviación estándar es simplemente la raíz cuadrada de la varianza. Se utiliza más comúnmente como una medida de dispersión de la varianza porque se mide en las mismas unidades que los elementos del conjunto de datos, mientras que la varianza se mide en cuadrado unidades.
Medidas de asociación
Medidas de asociación cuantificar la fuerza y la dirección de la relación entre dos conjuntos de datos. Estos son los dos más comúnmente utilizados medidas de asociación:
Ambas medidas se utilizan para mostrar cómo de cerca dos conjuntos de datos están relacionados entre sí. La principal diferencia entre ellos es las unidades en que se miden. La medida de correlación se define para asumir valores entre -1 y 1, lo que hace muy fácil interpretación.
Covarianza
los covarianza entre dos muestras se calcula como sigue:
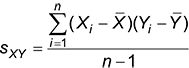
La covarianza entre dos poblaciones se calcula como sigue:
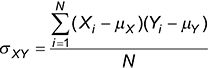
Correlación
los correlación entre dos muestras se calcula así:
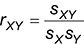
La correlación entre dos poblaciones se calcula así:
Cómo calcular la desviación estándar de un conjunto de datos estadísticos
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t
¿Cómo encontrar los momentos de la distribución binomial
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta
¿Cómo se mide la covarianza y correlación de muestras de datos
Medidas de asociación
Medidas de tendencia central
Medidas de dispersión Central