¿Cómo se mide la covarianza y correlación de muestras de datos
Al comparar las muestras de datos de diferentes poblaciones, dos de las medidas más populares de la asociación son covarianza y correlación. Covarianza y correlación muestran que las variables pueden tener una relación positiva, una relación negativa, o ninguna relación en absoluto.
Una muestra es una selección al azar de elementos elegidos de una población subyacente.
Covarianza de la muestra mide la fuerza y la dirección de la relación entre los elementos de dos muestras, y la correlación muestra se deriva de la covarianza. La covarianza muestral entre dos variables, X y Y, es
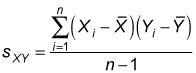
Esto es lo que significa cada elemento en esta ecuación:
sXY = La covarianza de la muestra entre las variables X y Y (los dos subíndices indican que esta es la covarianza de la muestra, no la desviación estándar de la muestra).

n = El número de elementos en ambas muestras.
yo = Un índice que asigna un número a cada elemento de la muestra, que van desde 1 a n.
Xyo = Un solo elemento en la muestra durante X.
Yyo = Un solo elemento en la muestra durante Y.
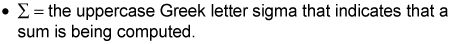
La covarianza muestra puede tener cualquier valor positivo o negativo.
Se calcula el correlación muestral (también conocida como la muestra coeficiente de correlación) Entre X y Y directamente desde la covarianza muestra con la siguiente fórmula:
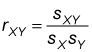
Los términos clave en esta fórmula son
rXY = Muestra correlación entre X y Y
sXY = Muestra covarianza entre X y Y
sX = Desviación estándar de la muestra X
sY = Desviación estándar de la muestra Y
La fórmula utilizada para calcular el coeficiente de correlación de la muestra asegura que su valor oscila entre -1 y 1.
Por ejemplo, supongamos que usted toma una muestra de rendimiento de las acciones de la Corporación Excelsior y el Adirondack Corporación de los años 2008 a 2012, como se muestra aquí:
| Año | Excelsior Corp. Declaración Anual (porcentaje) (X) | Adirondack Corp. Declaración Anual (porcentaje) (Y) |
|---|---|---|
| 2008 | 1 | 3 |
| 2009 | -2 | 2 |
| 2010 | 3 | 4 |
| 2011 | 0 | 6 |
| 2012 | 3 | 0 |
¿Cuáles son la covarianza y la correlación entre los rendimientos de las acciones? Para darse cuenta de eso, primero hay que encontrar la media de cada muestra. En este ejemplo, X representa los rendimientos de Excelsior y Y representa los rendimientos de Adirondack.
La media muestral de X es
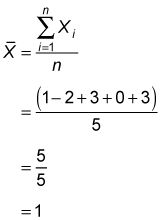
Usted obtiene la media muestral sumando todos los elementos de la muestra y luego dividiendo por el tamaño de la muestra. En este caso, los elementos de la muestra suman 5 y el tamaño de la muestra es 5. La división de estos números da una media de la muestra de 1.
La media muestral de Y es
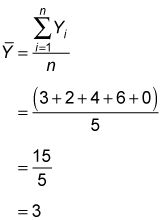
Esta tabla muestra los cálculos restantes para la covarianza de la muestra:

En la mesa, el
columna representa las diferencias entre cada retorno a Excelsior en la muestra y la muestra de significado similar, el
columna representa los mismos cálculos para Adirondack. Las entradas en el
la columna es igual al producto de las entradas en las dos columnas anteriores. La suma de las
columna indica el numerador de la fórmula de ejemplo covarianza:
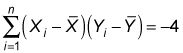
El denominador es igual al menos un tamaño de la muestra, que es 5 - 1 = 4. (Ambas muestras tienen cinco elementos, n = 5.) Por lo tanto, la covarianza muestra es igual
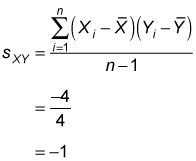
Para calcular el coeficiente de correlación de la muestra, dividir la covarianza de la muestra por el producto de la desviación estándar de la muestra de X y la desviación estándar de la muestra de Y:
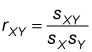
Usted encontrará la desviación estándar de la muestra de X calculando la varianza de la muestra de X y luego tomando la raíz cuadrada del resultado. La tabla muestra los cálculos de la varianza de la muestra de X.

En la mesa, el
columna representa las diferencias entre cada retorno a Excelsior en la muestra y la muestra el significado
columna representa el cuadrado diferencia entre cada vuelta al Excelsior y la media de la muestra. La suma de las
columna da el numerador en la fórmula de la varianza de la muestra. Se divide este número por el tamaño de la muestra menos (5 - 1 = 4) para obtener la varianza de la muestra de X:
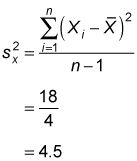
La desviación estándar de la muestra de X es la raíz cuadrada de 4,5, o
La tabla muestra los cálculos de la varianza de la muestra de Y.

Sobre la base de los cálculos de la tabla, la varianza de la muestra de Y es igual a
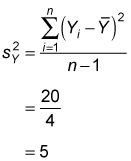
La desviación estándar de la muestra de Y es igual a la raíz cuadrada de 5, o
Sustituyendo estos valores en la fórmula de correlación muestra que da
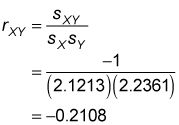
El resultado negativo muestra que hay una débil correlación negativa entre los rendimientos de las acciones de Excelsior y Adirondack. Si dos variables son perfectamente una correlación negativa (que siempre moverse en direcciones opuestas), su correlación será -1. Si dos variables son independiente (sin relación entre sí), su correlación será 0. La correlación entre los rendimientos de Excelsior y Adirondack de valores es un -0.2108, lo que indica que las dos variables muestran una ligera tendencia a moverse en direcciones opuestas.






