Aplicando la regla empírica (68-95-99,7) a un conjunto de datos estadísticos

los Regla empírica (68-95-99,7) dice que si la población de un conjunto de datos estadísticos tiene una distribución normal (donde los datos están en la forma de una curva de campana) con media poblacional # 181- y la desviación estándar

a continuación, cumplen las condiciones siguientes:

• Alrededor del 68% de los valores se encuentran dentro de 1 desviación estándar de la media (o entre la media menos 1 veces la desviación estándar, y la media más 1 veces la desviación estándar). En la notación estadística, esto se representa como

  

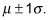
• Alrededor del 95% de los valores se encuentran dentro de 2 desviaciones estándar de la media (o entre la media menos 2 veces la desviación estándar y la media más 2 veces la desviación estándar). La notación estadística de esto es

  

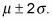
• Acerca de 99,7% de los valores se encuentran dentro de 3 desviaciones estándar de la media (o entre la media menos 3 veces la desviación estándar y la media más 3 veces la desviación estándar). Los estadísticos utilizan la siguiente notación para representar esto:

  

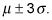
La regla empírica es también conocido como el 68-95-99,7 Regla, en correspondencia con esas tres propiedades. Se utiliza para describir una población en vez de una muestra, pero también se puede utilizar para ayudarle a decidir si una muestra de datos provenía de una distribución normal. Si una muestra es lo suficientemente grande y se puede ver que su histograma se ve cerca de una forma de campana, se puede comprobar para ver si los datos siguen las especificaciones 68-95-99,7 ciento. Si es así, es razonable concluir los datos provienen de una distribución normal.

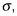
Esta figura ilustra los tres componentes de la regla empírica. La razón por la que muchos (aproximadamente 68%) de los valores se encuentran dentro de 1 desviación estándar de la media en la regla empírica es porque cuando los datos son en forma de campana, la mayoría de los valores se mounded arriba en el centro, cerca de la significa (como la figura muestra).

La adición de otro desviación estándar a cada lado de la media aumenta el porcentaje a partir de 68 a 95, que es un gran salto y da una buena idea de dónde " más " de los datos se encuentran. La mayoría de los investigadores se quedan con el rango de 95% (en lugar de 99,7%) para informar de sus resultados, porque el aumento de la gama de 3 desviaciones estándar a cada lado de la media (en lugar de sólo 2) no parece que vale la pena, sólo para recoger otro 4,7% de los valores.

La regla empírica que dice acerca de ¿qué porcentaje de los valores se encuentran dentro de un cierto rango de la media. Estos resultados son sólo aproximaciones, y que sólo se aplican si los datos siguen una distribución normal. Sin embargo, la regla empírica es un resultado importante en las estadísticas debido a que el concepto de " a salir alrededor de dos desviaciones estándar para obtener el 95% de los valores " es uno que se ve mencionado muchas veces con intervalos de confianza y pruebas de hipótesis.