La desviación estándar, varianza, y el coeficiente de variación de los datos bioestadística

categoría Educación y lenguas / Ciencia / Biología

los desviacion estandar (generalmente abreviado SD, sd, o solo s) De un montón de números te dice lo mucho que los números individuales tienden a ser diferentes (en cualquier dirección) de la media. Se calcula como sigue:

image0.jpg

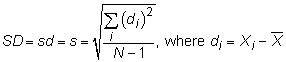
Esta fórmula está diciendo que se calcula la desviación estándar de un conjunto de N números (Xyo) Restando la media de cada valor para obtener el desviación (dyo) De cada valor de la media, elevar al cuadrado cada una de estas desviaciones, sumando el

image1.jpg

términos, dividiendo por N - 1 y, a continuación, tomar la raíz cuadrada.

Esta es casi idéntica a la fórmula para la desviación de la raíz cuadrática media de los puntos de la media, excepto que tiene N - 1 en el denominador en lugar de N. Esta diferencia se debe a que la media de la muestra se utiliza como una aproximación de la verdadera media de la población (que no sabe). Si la verdadera media estaban disponibles para usar, el denominador sería N.

Cuando se habla de distribuciones de la población, el SD describe la anchura de la curva de distribución. La figura muestra tres distribuciones normales. Todos ellos tienen una media de cero, pero tienen diferentes desviaciones estándar y, por tanto, diferentes anchuras. Cada curva de distribución tiene un área total de exactamente 1,0, por lo que la altura del pico es menor cuando el SD es más grande.

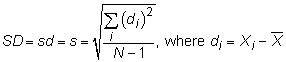
image2.jpg

Para un ejemplo IQ (84, 84, 89, 91, 110, 114 y 116), donde la media es de 98,3, se calcula el SD de la siguiente manera:

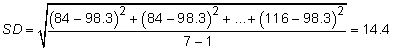
image3.jpg

Las desviaciones estándar son muy sensibles a los valores extremos (outliers) en los datos. Por ejemplo, si el valor más alto en el conjunto de datos IQ había sido 150 en lugar de 116, la SD habría subido 14,4 a 23,9.

Varias otras medidas útiles de dispersión están relacionados con la SD:

  • Varianza: los desacuerdo es simplemente el cuadrado de la SD. Para el ejemplo IQ, la varianza = 14,42 = 207,36.

  • Coeficiente de variación: los coeficiente de variación (CV) es la SD dividida por la media. Para el ejemplo de IQ, CV = 14,4 / 98,3 = 0,1465, o 14,65 por ciento.



Artículos Relacionados

Sobre el autor
Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t Cómo calcular el valor esperado, la varianza y la desviación estándar de una distribución t

Distribuciones de probabilidad, incluyendo la distribución t, tienen varios momentos, incluyendo el valor esperado, la varianza y la desviación estándar (una momento es una medida resumen de una distribución de probabilidad):El primer momento de…

¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial ¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial

Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes…

¿Cómo encontrar los momentos de la distribución binomial ¿Cómo encontrar los momentos de la distribución binomial

Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…

Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta

Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…

¿Cómo interpretar la desviación estándar de un conjunto de datos estadísticos ¿Cómo interpretar la desviación estándar de un conjunto de datos estadísticos

La desviación estándar puede ser difícil de interpretar como un solo número por sí solo. Básicamente, una pequeña desviación estándar significa que los valores de un conjunto de datos estadísticos se encuentran cerca de la media del…

¿Cómo medir los momentos de la f-distribución ¿Cómo medir los momentos de la f-distribución

Momentos son medidas de resumen de una distribución de probabilidad e incluyen el valor esperado, la varianza y la desviación estándar. Puede utilizar estos valores para medir hasta qué punto los grados de libertad afecta a la distribución…

¿Cómo decirle a un z-distribución de una distribución t ¿Cómo decirle a un z-distribución de una distribución t

Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…

¿Cómo se utilizan los valores z en las estadísticas ¿Cómo se utilizan los valores z en las estadísticas

Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…

Medidas de dispersión Central Medidas de dispersión Central

Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…

La desviación estándar y la varianza La desviación estándar y la varianza

Los problemas aquí se centran en calcular, interpretar y comparar la desviación estándar y la varianza en las estadísticas básicas. Resuelve los siguientes problemas sobre la desviación estándar y la varianza.Ejemplos de preguntas¿Qué mide…

Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos

Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…

Estadísticas para grandes datos para los maniquíes Estadísticas para grandes datos para los maniquíes

Medidas de tendencia central muestran el centro de un conjunto de datos. Tres de las medidas más utilizadas de tendencia central son la media, la mediana y la moda.SignificarSignificar es otra palabra para la media. Esta es la fórmula para el…

» » » » La desviación estándar, varianza, y el coeficiente de variación de los datos bioestadística