¿Cómo afecta el tamaño de la muestra error estándar
El tamaño (n) De una muestra estadística afecta el error estándar para esa muestra. Porque n se encuentra en el denominador de la fórmula error estándar, el error estándar disminuye a medida n aumenta. Tiene sentido que el tener más datos da una menor variación (y más precisión) en sus resultados.
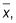
Suponer X es el tiempo que le toma a un trabajador de oficina para escribir y enviar una carta de recomendación, y decir X tiene una distribución normal con una media de 10,5 minutos y desviación estándar de 3 minutos. La curva inferior en la figura anterior muestra la distribución de X, los tiempos individuales para todos los trabajadores de oficina en la población. De acuerdo con la regla empírica, casi todos los valores están dentro de 3 desviaciones estándar de la media (10,5) - entre 1,5 y 19,5.
Ahora toma una muestra aleatoria de 10 empleados de oficina, medir sus tiempos, y encontrar el promedio,
cada vez. Repita este proceso una y otra, y graficar todos los posibles resultados de todas las muestras posibles. La curva de media en la figura muestra la imagen de la distribución muestral de
Tenga en cuenta que todavía está centrada a 10.5 (que se espera), pero su variabilidad se SMALLER- el error estándar en este caso es
(un poco menos de 3 minutos, la desviación estándar de los tiempos individuales).
En cuanto a la figura, los tiempos medios para muestras de 10 trabajadores administrativos están más cerca de la media (10,5) que los tiempos individuales. Eso es porque los tiempos promedio no varían tanto de una muestra a veces como individuales varían de persona a persona.
Ahora tome todas las posibles muestras aleatorias de 50 trabajadores administrativos y encontrar su significa- se muestra la distribución de muestreo de la curva más alta de la figura. El error estándar de
Usted puede ver los tiempos promedio de 50 trabajadores administrativos son aún más cerca de 10.5 que los de 10 trabajadores administrativos. Por la regla empírica, casi todos los valores caen entre 10,5-3 (0,42) = 9.24 y 10.5 + 3 (0,42) = 11,76. Muestras más grandes tienden a ser un reflexiones más precisas de la población, por lo tanto, sus medias de la muestra tienen más probabilidades de estar más cerca de la media de la población - por lo tanto una menor variación.
¿Por qué tener más precisión alrededor de la media importante? Porque a veces no sabes la media poblacional, sino que determinar lo que es, o al menos acercarse a ella como sea posible. ¿Como puedes hacer eso? Al tomar una gran muestra aleatoria de la población y la búsqueda de su media. Usted sabe que su media de la muestra estará cerca de la población de hecho significaría si su muestra es grande, tal como muestra la figura (suponiendo que sus datos se recogen correctamente).
-
Aplicando la regla empírica (68-95-99,7) a un conjunto de datos estadísticos -
El empleo de la regla empírica en problemas estadísticos -
Encontrar la desviación estándar de una muestra estadística -
Cómo una distribución normal afecta a la forma de una distribución de muestreo -
Cómo desviación estándar de población afecta error estándar -
Cómo el número de grados de libertad afecta a la gráfica de una distribución t
Cómo calcular un intervalo de confianza para una media poblacional cuando se conoce la desviación estándar Si conoce la desviación estándar de una población, entonces se puede calcular un intervalo de confianza (IC) para la media o promedio, de esa población. Cuando una característica estadística que está siendo medido (tales como ingresos, IQ,…
Cómo calcular un intervalo de confianza para una media poblacional con una desviación estándar desconocida y / o pequeño tamaño de la muestra Usted puede calcular un intervalo de confianza (IC) para la media o promedio, de una población, incluso si la desviación estándar es desconocida o el tamaño de la muestra es pequeño. Cuando una característica estadística que está siendo…
Cómo calcular el margen de error para una media muestral Cuando una pregunta de investigación pide a encontrar una estadística media de la muestra (o promedio), es necesario reportar un margen de error, o el Ministerio de Educación, para la media de la muestra. La fórmula general para el margen de…
¿Cómo encontrar probabilidades para una media muestral En las estadísticas, usted puede encontrar fácilmente las probabilidades de una media muestral si tiene una distribución normal. Incluso si no tiene una distribución normal, o la distribución no se conoce, se puede encontrar probabilidades si…
¿Cómo encontrar la distribución de muestreo de una proporción de la muestra Si utiliza un tamaño suficiente gran muestra estadística, se puede aplicar el teorema del límite central (CLT) a una proporción de la muestra para los datos categóricos para encontrar su distribución muestral. los proporción de la población,…
Cómo identificar una distribución muestral En estadística, una distribución de muestreo se basa en promedios de la muestra en lugar de los resultados individuales. Esto hace que sea diferente de una distribución. He aquí por qué: A variable al azar es una característica de interés que…
Cómo identificar la notación para la media y la varianza de una variable aleatoria discreta Dos de los términos más importantes en las estadísticas son la media y la varianza, y por lo que tienen que ser capaces de identificar sus anotaciones cuando se trabaja con variables aleatorias discretas.los significar de una variable aleatoria…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
Cómo utilizar el t-test para manejar pequeñas muestras y las desviaciones estándar desconocidos Cuando se utiliza una prueba estadística para una media poblacional, hay dos casos en los que debe utilizar el t-distribución en lugar de la Z-distribución. El primer caso es donde el tamaño de la muestra es pequeño (por debajo de 30 o así), y…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Estadísticamente calcular tamaño de la muestra En el diseño de un estudio, el tamaño de la muestra es una consideración importante, ya que cuanto mayor sea el tamaño de la muestra, más datos que usted tiene, y cuanto más precisos serán los resultados (suponiendo datos de alta calidad). Si…
La exactitud y la precisión en términos de la distribución de muestreo La idea de una distribución de muestreo está en el corazón de los conceptos de exactitud y precyosión. Imagine un escenario en el que un experimento (como un ensayo clínico o un estudio) se lleva a cabo una y otra vez un gran número de veces,…