¿Cómo encontrar probabilidades para una media muestral
En las estadísticas, usted puede encontrar fácilmente las probabilidades de una media muestral si tiene una distribución normal. Incluso si no tiene una distribución normal, o la distribución no se conoce, se puede encontrar probabilidades si el tamaño de la muestra, n, es lo suficientemente grande.
La distribución normal es una distribución muy amable que tiene una mesa para encontrar probabilidades y cualquier otra cosa que usted necesita. Por ejemplo, usted puede encontrar probabilidades para
mediante la conversión de la
a una z-valor y las probabilidades de encontrar utilizando el Z-tabla (véase más abajo).
La fórmula de conversión general a partir de
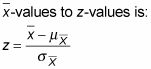
Sustituyendo los valores apropiados de la media y el error estándar de
la fórmula de conversión se convierte en:
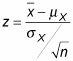
No se olvide de dividir por la raíz cuadrada de n en el denominador de z. Siempre dividir por la raíz cuadrada de n cuando la pregunta se refiere a la promedio de El X-los valores.
Por ejemplo, supongamos X es el tiempo que tarda un trabajador administrativo elegido al azar en una oficina para escribir y enviar una carta tipo de recomendación. Suponer X tiene una distribución normal, y asumir la media es 10,5 minutos y la desviación estándar de 3 minutos. Se toma una muestra aleatoria de 50 trabajadores administrativos y medir sus tiempos. ¿Cuál es la probabilidad de que su tiempo promedio es de menos de 9,5 minutos?
Esta pregunta se traduce en hallazgo
Como X tiene una distribución normal para empezar, ya sabes
también tiene un exacto (no aproximado) de distribución normal. Convertir a z, usted obtiene:
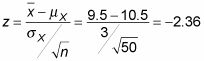
¿Así que quieres P (Z lt; -2,36).
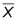
Utilizando el anterior Z-mesa, usted encuentra que P (Z lt; -2,36) = 0,0091. Así que la probabilidad de que una muestra aleatoria de 50 empleados de oficina promedio menos de 9.5 minutos para completar esta tarea es de 0,91% (muy pequeño).
¿Cómo encuentras probabilidades para
si X es no normal o desconocido? Como resultado de teorema del límite central (CLT), la distribución de X puede ser no normal o incluso desconocido y mientras n es lo suficientemente grande, todavía se puede encontrar aproximado probabilidades para
utilizando la normal estándar (Z-) la distribución y el proceso descrito anteriormente. Es decir, convertir a una z-valorar y encontrar probabilidades aproximadas utilizando el Z-mesa.
Cuando se utiliza la CLT para encontrar una probabilidad de
(es decir, cuando la distribución de X es no normal o se desconoce), asegúrese de decir que la respuesta es un aproximación. También quiere decir que la respuesta aproximada debe estar cerca porque tienes una lo suficientemente grande n utilizar el CLT. (Si n no es lo suficientemente grande para la CLT, puede utilizar la t-distribución en muchos casos.)
-
Distribuciones de probabilidad en el análisis estadístico de datos grande -
Econometría y la distribución t -
Poniendo las variables en la misma escala: la distribución normal estándar (z) - Estadísticas de las empresas: rendimientos de los activos de modelado con distribución normal
-
Diferenciar entre distribuciones de probabilidad discretas y continuas -
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una muestra grande
Cómo una distribución normal afecta a la forma de una distribución de muestreo En las estadísticas, cuando la distribución original para una población X es normal, entonces usted también puede asumir que la forma de la distribución de muestreo, oTambién será normal, independientemente del tamaño de muestra n.Por…
¿Cómo se ve afectada una distribución de muestreo cuando la distribución no es normal En estadística, si una población X tiene cualquier distribución que es no lo normal, o si su distribución es desconocida, no se puede decir de forma automática la distribución de las medias de la muestratiene una distribución normal. Pero…
¿Cómo afecta el tamaño de la muestra error estándar El tamaño (n) De una muestra estadística afecta el error estándar para esa muestra. Porque n se encuentra en el denominador de la fórmula error estándar, el error estándar disminuye a medida n aumenta. Tiene sentido que el tener más datos da…
Cómo el número de grados de libertad afecta a la gráfica de una distribución t Una de las propiedades interesantes de la distribución t es que cuanto mayor es el grado de libertad, más de cerca la distribución t se asemeja a la distribución normal estándar. A medida que los grados de libertad aumenta, el área en las…
Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central Puede utilizar el teorema del límite central para convertir una distribución muestral de una variable aleatoria normal estándar. Con base en el teorema del límite central, si dibuja muestras de una población que es mayor o igual a 30, entonces…
¿Cómo encontrar percentiles de una distribución t Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…
¿Cómo encontrar probabilidades para z con la mesa de z Puede utilizar el Z-mesa para encontrar un conjunto completo de "-menos que" las probabilidades para una amplia gama de z-los valores. Para utilizar el Z-tabla para encontrar las probabilidades de una muestra estadística con una normal estándar…
¿Cómo encontrar probabilidades estadísticas en una distribución normal Si su muestra estadística tiene una distribución normal (X), Entonces usted puede utilizar el Z-mesa para encontrar la probabilidad de que algo va a ocurrir dentro de un conjunto definido de parámetros. Por ejemplo, usted podría mirar a la…
¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n Si usted está trabajando de una gran muestra estadística, a continuación, la solución de problemas utilizando la distribución binomial puede parecer desalentador. Sin embargo, en realidad hay una manera muy fácil para aproximar la…
¿Cómo encontrar la distribución de muestreo de una proporción de la muestra Si utiliza un tamaño suficiente gran muestra estadística, se puede aplicar el teorema del límite central (CLT) a una proporción de la muestra para los datos categóricos para encontrar su distribución muestral. los proporción de la población,…
¿Cómo decirle a un z-distribución de una distribución t Aunque la normal (Z-) Distribución y t-distribución son similares, se ven diferentes entre sí y se utilizan para diferentes fines estadísticos. La distribución normal es que la distribución en forma de campana conocida cuya media esy cuya…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…