¿Cómo encontrar probabilidades para z con la mesa de z

categoría Educación y lenguas / Matemáticas / Estadísticas

Puede utilizar el Z-mesa para encontrar un conjunto completo de "-menos que" las probabilidades para una amplia gama de z-los valores. Para utilizar el Z-tabla para encontrar las probabilidades de una muestra estadística con una normal estándar (Z-) La distribución, haga lo siguiente:

  1. Ir a la fila que representa el dígito y el primer dígito después del punto decimal (el dígito décimas) de su z-valor.

  2. Ir a la columna que representa el segundo dígito después del punto decimal (el dígito centésimas) de su z-valor.

  3. Intersección de la fila y la columna de los pasos 1 y 2.

    Este resultado representa p(Z lt; z), Que la variable aleatoria la probabilidad Z es menor que el valor z (también conocido como el porcentaje de z-valores que son menores que la dada z valor).

Por ejemplo, suponga que desea encontrar p(Z lt; 2,13). Usando el Z-tabla de abajo, se encontró la fila para 2.1 y la columna de 0.03. Intersección esa fila y columna para encontrar la probabilidad: 0,9834. Por Consiguiente p(Z lt; 2,13) ​​= 0,9834.

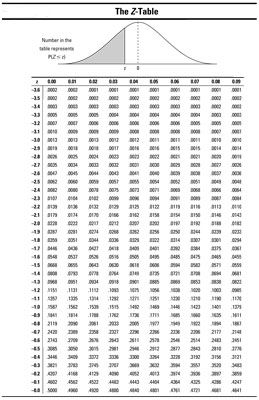
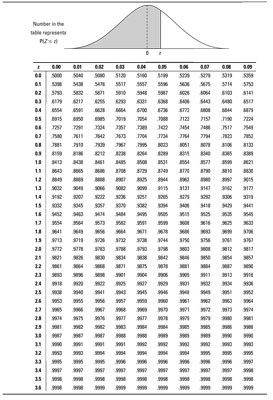
imagen0.jpgimage1.jpg

Tomando nota de que el área total bajo cualquier curva normal (incluyendo la curva normal estandarizada) es 1, se deduce que p(Z lt; 2,13) ​​+ p(Z > 2,13) ​​= 1. Por Consiguiente, p(Z > 2,13) ​​= 1 - p(Z lt; 2,13), que es igual a 1 - 0.9834 que es igual a 0,0166.

Suponga que desea buscar p(Z lt; -2,13). Usted encuentra la fila de -2,1 y la columna de 0.03. Intersección de la fila y la columna y te encuentras con que los medios 0.0166- p(Z lt; -2,13) ​​= 0,0166. Observe que esto le sucede a ser igual p(Z> 2,13) ​​.La razón de esto es 'debido a la distribución normal es simétrica. Así que la cola de la curva de abajo -2,13 representando p(Z lt; -2.13) Se ve exactamente como la cola por encima de 2,13 que representa p(Z > 2,13).



Artículos Relacionados

Sobre el autor
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una pequeña muestra Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una pequeña muestra

Cuando se utiliza una pequeña muestra para probar una hipótesis acerca de una media poblacional, se toma el valor crítico resultante o los valores de la distribución t de Student. Para una prueba de dos colas, el valor crítico esy n representa…

Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una muestra grande Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una muestra grande

En estadística, una amplia muestra tiene un tamaño mayor o igual a 30. Cuando se utiliza una gran muestra para probar una hipótesis acerca de una media poblacional, el valor o valores críticos resultante de dos colas de la distribución normal…

Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central Cómo convertir una distribución de muestreo a una variable aleatoria normal estándar usando el teorema del límite central

Puede utilizar el teorema del límite central para convertir una distribución muestral de una variable aleatoria normal estándar. Con base en el teorema del límite central, si dibuja muestras de una población que es mayor o igual a 30, entonces…

¿Cómo encontrar un percentil de una distribución normal ¿Cómo encontrar un percentil de una distribución normal

Un problema de distribución normal populares implica percentiles hallazgo para X. Es decir, se le da el porcentaje o probabilidad estadística de estar en o por debajo de un cierto X-valor, y usted tiene que encontrar el X-valor que corresponde a…

¿Cómo encontrar percentiles de una distribución t ¿Cómo encontrar percentiles de una distribución t

Cuando usted quiere encontrar percentiles para un t-distribución, se puede utilizar el t-mesa. LA percentil es un número en una distribución estadística cuya menos que la probabilidad es la porcentaje- dada por ejemplo, el percentil 95 de la…

¿Cómo encontrar probabilidades estadísticas en una distribución normal ¿Cómo encontrar probabilidades estadísticas en una distribución normal

Si su muestra estadística tiene una distribución normal (X), Entonces usted puede utilizar el Z-mesa para encontrar la probabilidad de que algo va a ocurrir dentro de un conjunto definido de parámetros. Por ejemplo, usted podría mirar a la…

¿Cómo encontrar los valores críticos para una hipótesis de ANOVA utilizando el f-mesa ¿Cómo encontrar los valores críticos para una hipótesis de ANOVA utilizando el f-mesa

Usted puede encontrar los valores críticos para una hipótesis de ANOVA utilizando la mesa F. Debido a que la distribución F se basa en dos tipos de grados de libertad, hay una tabla para cada posible valor de alfa (el nivel de significación).La…

¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n ¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n

Si usted está trabajando de una gran muestra estadística, a continuación, la solución de problemas utilizando la distribución binomial puede parecer desalentador. Sin embargo, en realidad hay una manera muy fácil para aproximar la…

¿Cómo encontrar incondicionales, o marginales, probabilidades ¿Cómo encontrar incondicionales, o marginales, probabilidades

Un incondicional, o marginal, la probabilidad es uno donde los eventos (posibles resultados) son independientes entre sí. Cuando se crea un tabla de probabilidad conjunta, la probabilidad incondicional de un evento aparece como un total de fila o…

¿Cómo encontrar t *-valores para los intervalos de confianza ¿Cómo encontrar t *-valores para los intervalos de confianza

Intervalos de confianza estimación de los parámetros de población, tales como la media poblacional, mediante el uso de una estadística (por ejemplo, la media de la muestra) más o menos un margen de error. Para calcular el margen de error para…

Cómo utilizar el t-mesa para resolver los problemas de estadística Cómo utilizar el t-mesa para resolver los problemas de estadística

los t-mesa (para el t-distribución) es diferente de la Z-mesa (para el Z-distribución) - asegúrese de entender los valores de la primera y última filas. Encontrar probabilidades para varios t-distribuciones, utilizando el t-mesa, es una valiosa…

Cómo utilizar el t-test para manejar pequeñas muestras y las desviaciones estándar desconocidos Cómo utilizar el t-test para manejar pequeñas muestras y las desviaciones estándar desconocidos

Cuando se utiliza una prueba estadística para una media poblacional, hay dos casos en los que debe utilizar el t-distribución en lugar de la Z-distribución. El primer caso es donde el tamaño de la muestra es pequeño (por debajo de 30 o así), y…

» » » » ¿Cómo encontrar probabilidades para z con la mesa de z