¿Cómo encontrar un percentil de una distribución normal

Un problema de distribución normal populares implica percentiles hallazgo para X. Es decir, se le da el porcentaje o probabilidad estadística de estar en o por debajo de un cierto X-valor, y usted tiene que encontrar el X-valor que corresponde a la misma. Por ejemplo, si usted sabe que las personas cuyos puntajes de golf estaban en el 10% más bajo que ir a un torneo, usted puede preguntarse lo que el punto de corte fue- ese aspecto representaría el percentil 10.

Un percentil no es un por ciento. Un porcentaje es un número entre 0 y 100 y un percentil es un valor de X (una altura, un coeficiente intelectual, una calificación de la prueba, y así sucesivamente).

Ciertos percentiles son tan populares que tienen sus propios nombres y su propia notación. Los tres percentiles "con nombre" son Q₁ - el primer cuartil, o la percentile- 25a Q₂ - el segundo cuartil (también conocido como el mediana o el percentil 50) - y Q₃ - el tercero cuartil o el 75 por ciento.

Estos son los pasos para encontrar cualquier percentil de una distribución normal X:

1. 1a.If te dan la probabilidad (por ciento) menos de X y es necesario encontrar X, traducir esto como: Buscar la dónde p(X lt; la) = p (y p es la probabilidad dada).

   Es decir, encontrar el pº percentil para X. Vaya al paso 2.

2. 1b.If te dan la probabilidad (por ciento) mayor que X y es necesario encontrar X, traducir esto como: Buscar b dónde p(X > b) = p (y p es dado).

   Vuelva a escribir esto como un percentil problema (menos de): Buscar b dónde p(X lt; b) = 1 - p. Esto significa encontrar el (1 - p) percentil para X.

3. Encuentra el percentil correspondiente para Z mirando en el cuerpo de la Z-tabla (véase más abajo) y la búsqueda de la probabilidad de que es más cercana a p (de la etapa 1a) o 1 - p (del Paso 1b).

   Encuentra la fila y la columna de esta probabilidad está en (usando la tabla al revés). Este es el deseado z-valor.

4. Cambiar el z-valorar de nuevo en un X-valor (unidades originales) mediante el uso de

   

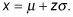
   Usted (¡por fin!) Ha encontrado el percentil deseado para X. La fórmula en este paso es sólo una reescritura de la z-fórmula,

   

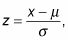
   así que ha resolverse para X.

He aquí un ejemplo: Supongamos que usted entra en un concurso de pesca. El concurso tiene lugar en un estanque donde las longitudes de pescado tienen una distribución normal con una media de 16 pulgadas y una desviación estándar de 4 pulgadas. Ahora supongamos que usted quiere saber qué longitud se cumple el 10 por ciento de todas las longitudes de peces en el estanque. Qué percentil estás buscando?

Estar en el 10 por ciento significa que tiene una probabilidad "-menos" que es igual a 10 por ciento, y que están en el percentil 10.

Ahora vaya al paso 1a y traducir el problema. En este caso, debido a que está tratando con una situación "-menos", que desea buscar X de tal manera que p(X lt; X) = 0,10. Esto representa el percentil 10 para X. La siguiente figura muestra una imagen de esta situación.

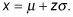
Ahora vaya al paso 2, que dice para encontrar el percentil 10 para Z.

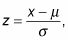
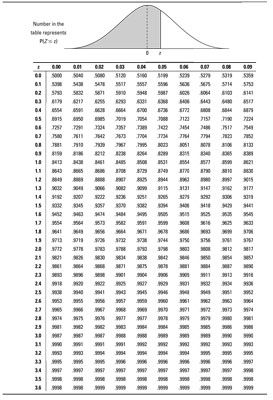
Mirando en el cuerpo de la Z-mesa, la probabilidad más cercana a 0,10 es 0,1003, que cae en la fila z = -1.2 Y la columna de 0.08. Eso significa que el percentil 10 para Z es -1.28- por lo que un pescado cuya longitud es de 1,28 desviaciones estándar por debajo de la media se conmemora el 10 por ciento de todas las longitudes de peces en el estanque.

Pero exactamente cuánto tiempo es que los peces, en pulgadas? En el paso 3, se cambia el zvalorar de nuevo a un X-valor (longitud del pez en pulgadas), utilizando el z-fórmula para resolver X- usted obtiene X = 16 + -1,28 [4] = 10,88 pulgadas. Así 10.88 pulgadas marca el 10 por ciento de las longitudes de peces. El diez por ciento de los peces son más cortos que eso.