¿Cómo encontrar probabilidades estadísticas en una distribución normal

Si su muestra estadística tiene una distribución normal (X), Entonces usted puede utilizar el Z-mesa para encontrar la probabilidad de que algo va a ocurrir dentro de un conjunto definido de parámetros. Por ejemplo, usted podría mirar a la distribución de longitudes de peces en un estanque para determinar cómo será la probabilidad de coger una cierta longitud de los peces.

Sigue estos pasos:

1. Haz un dibujo de la distribución normal.

2. Traducir el problema en uno de los siguientes: p(X lt; la), p(X > b), O p(la lt; X lt; b). Sombra en la zona en la foto.

3. Estandarizar la (y / o b) A una z-calificar usando el z-fórmula:

4. Busque el z-anotar en el Z-tabla (ver más abajo) y encontrar su correspondiente probabilidad.

   a.Find la fila de la tabla correspondiente al primer dígito (dígito de las unidades) y el primer dígito después del punto decimal (el dígito décimas).

   b.Find la columna correspondiente al segundo dígito después del punto decimal (el dígito centésimas).

   c.Intersect la fila y columna de los pasos (a) y (b).

5. 5a.If necesita una "menos-que" probabilidad - es decir, p(X lt; la) - ya terminaste.

6. 5b.If quieres un "mayor que" probabilidad - es decir, p(X > b) - Tener uno menos el resultado del paso 4.

7. 5c.If necesita una "entre dos valores de" probabilidad - es decir, p(la lt; X lt; b) - Hacer los pasos 1-4 para b (el mayor de los dos valores) y de nuevo para la (el menor de los dos valores), y restar los resultados.

La probabilidad de que X es igual a cualquier valor individual es 0 para cualquier variable aleatoria continua (como la normal). Esto se debe a variables aleatorias continuas consideran probabilidad como área bajo la curva, y no hay área bajo una curva en un solo punto. Esto no es cierto de variables aleatorias discretas.

Supongamos, por ejemplo, que usted entra en un concurso de pesca. El concurso tiene lugar en un estanque donde las longitudes de peces tienen una distribución normal con media

y la desviación estándar

• Problema 1: ¿Cuál es la probabilidad de que la captura de un pez pequeño - por ejemplo, menos de 8 pulgadas?

• Problema 2: Supongamos que un premio se ofrece para cualquier pez de más de 24 pulgadas. ¿Cuál es la probabilidad de ganar un premio?

• Problema 3: ¿Cuál es la probabilidad de captura de un pez de 16 a 24 pulgadas?

Para resolver estos problemas utilizando los pasos anteriores, primero hacer un dibujo de la distribución normal a la mano.

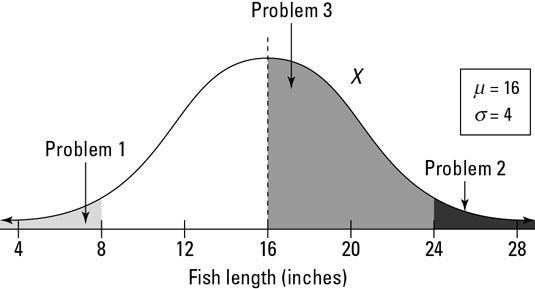
Esta figura muestra una imagen de X's la distribución de longitudes de peces. Usted puede ver dónde están los números de interés (8, 16, y 24) caen.

A continuación, traducir cada problema a notación probabilidad. Problema 1 es realmente pidiendo que encontrar p(X lt; 8). Para el problema 2, desea p(X > 24). Y el problema 3 está buscando p(16 lt; X lt; 24).

Paso 3 dice cambiar la X-valores a zvalores utilizando el zfórmula:

Para el problema 1 del ejemplo de pescado, tiene lo siguiente:

Del mismo modo para el problema 2, p(X > 24) se convierte

Y el problema 3 traduce del p(16 lt; X lt; 24) a

La siguiente figura muestra una comparación de la X-distribución y Z-la distribución de los valores X = 8, 16, y 24, que a estandarizar z = -2, 0, y 2, respectivamente.

Ahora que ha cambiado X-valores a zvalores, se mueven al paso 4 y el cálculo de probabilidades para los zvalores utilizando el Z-mesa.

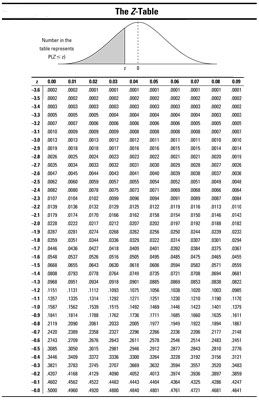
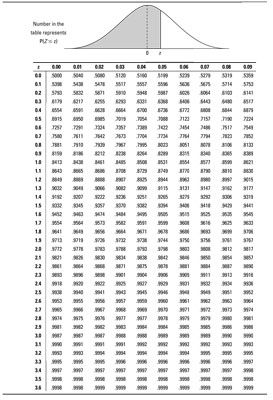
En el problema 1 del ejemplo de pescado, que desea p(Z lt; -2) - Ir a la Z-mesa y mirar a la fila de -2,0 y la columna de 0,00, ellos se cruzan, y te encuentras 0,0228 - de acuerdo con el Paso 5a, ya está hecho. La probabilidad de un pez de ser menos de 8 pulgadas es igual a 0.0228.

Para el problema 2, encontrar p(Z > 2,00). Debido a que es un "mayor que" el problema, esto exige Paso 5b. Para ser capaz de utilizar el Z-tabla, es necesario volver a escribir esto en términos de un "menos que" comunicado. Debido a que toda la probabilidad para el Z-la distribución es igual a 1, ya sabes p(Z > 2.00) = 1 - p(Z lt; 2.00) = 1 - ,9772 = 0,0228 (utilizando el Z-mesa). Por lo tanto, la probabilidad de que un pez es mayor que 24 pulgadas también es 0,0228. (Nota: Las respuestas a los problemas 1 y 2 son los mismos porque el Z-distribución es symmetric- referirse a la primera figura.)

En el problema 3, a encontrar p(0 lt; Z lt; 2.00) - esto requiere el paso 5c. Primer hallazgo p(Z lt; 2,00), que es desde el 0,9772 Z-mesa. A continuación, busque p(Z lt; 0), que es desde el 0,5000 Z-mesa. Reste ellos para obtener 0,9772 hasta 0,5000 = 0,4772. La probabilidad de un pez de ser entre 16 y 24 pulgadas es 0.4772.

los Z-mesa no enumera todos los valores posibles de Z- sólo los lleva a dos dígitos después del punto decimal. Utilice la más cercana a la que usted necesita. Y al igual que en un avión en la salida más cercana puede estar detrás de ti, el más cercano z-valor puede ser el que es más bajo que el que necesita.