¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n

Si usted está trabajando de una gran muestra estadística, a continuación, la solución de problemas utilizando la distribución binomial puede parecer desalentador. Sin embargo, en realidad hay una manera muy fácil para aproximar la distribución binomial, como se muestra en este artículo.

He aquí un ejemplo: supongamos que usted lanza una moneda al aire 100 veces y se deja X igual al número de cabezas. ¿Cuál es la probabilidad de que X es mayor que 60?

En una situación como ésta, donde n es grande, los cálculos pueden obtener difícil de manejar y la tabla binomial se queda sin números. Así que si no hay tecnología disponible (como cuando se toma un examen), ¿qué puede hacer usted para encontrar una probabilidad binomial? Resulta que, si n es lo suficientemente grande, puede utilizar la distribución normal de encontrar una respuesta aproximada muy estrecha con mucho menos trabajo.

Pero, ¿qué entendemos por n ser "suficientemente grande"? Para determinar si n es lo suficientemente grande como para utilizar lo que los estadísticos llaman el aproximación normal a la binomial, ambas de las siguientes condiciones deben contener:

Para encontrar la aproximación normal a la distribución binomial cuando n es grande, utilice los siguientes pasos:

1. Verifique si n es lo suficientemente grande para utilizar la aproximación normal mediante la comprobación de las dos condiciones apropiadas.

   Para la cuestión de la moneda de volteo anterior, se cumplen las condiciones, porque n # 8727- p = 100 # 8727- 0,50 = 50, y n # 8727- (1 - p) = 100 # 8727- (1-0,50) = 50, ambos de los cuales son al menos 10. Así que adelante con la aproximación normal.

2. Traducir el problema en una declaración de probabilidad acerca de X.

   En este ejemplo, usted necesita encontrar p(X > 60).

3. Estandarizar la X-valor a un z-valor, utilizando el z-fórmula:

   

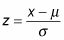
   Para la media de la distribución normal, utilice

   

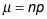
   (la media de la binomial), y para la desviación estándar

   

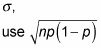
   (la desviación estándar de la binomial).

   Así, en el ejemplo de la moneda de volteo, usted tiene

   

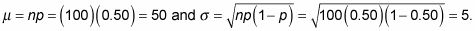
   A continuación, poner estos valores en la z-fórmula para obtener

   

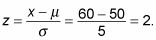
   Para resolver el problema, es necesario encontrar p(Z > 2).

   En un examen, no verá

   

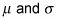
   en el problema cuando se tiene una distribución binomial. Sin embargo, usted sabe las fórmulas que permiten calcular ambos usando n y p (ambos de los cuales será dada en el problema). Sólo recuerde que usted tiene que hacer ese paso extra para calcular el

   

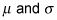
   necesaria para el z-fórmula. Ahora puede proceder como lo haría normalmente para cualquier distribución normal.

4. Busque el z-anotar en el Z-mesa y encontrar su correspondiente probabilidad.

5. a. Encuentra la fila de la tabla correspondiente al primer dígito (un dígito) y el primer dígito después del punto decimal (el dígito décimas).

6. b. Encuentra la columna correspondiente al segundo dígito después del punto decimal (el dígito centésimas).

7. c. Intersección la fila y columna de los pasos (a) y (b).

   Continuando con el ejemplo, a partir de la z-valor de 2,0, se obtiene una probabilidad correspondiente de 0.9772 de la Z-mesa.

   

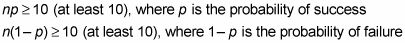
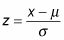
8. Seleccione uno de los siguientes.

9. a. Si usted necesita un "menos que" probabilidad - es decir, p (X lt; a) - ya está.

10. b. Si quieres un "mayor que" probabilidad - es decir, p (X> b) - tener uno menos el resultado del paso 4.

    Recuerde, este ejemplo está en busca de un mayor de probabilidad ("¿Cuál es la probabilidad de que X - el número de lanzamientos - es mayor que 60"). Conexión del resultado del paso 4, se encuentra p (Z> 2,00) = 1 a 0,9772 = 0,0228. Así que la probabilidad de obtener más de 60 cabezas en 100 lanzamientos de una moneda es sólo un 2,28 por ciento. (En otras palabras, no apostaría por ello.)

11. c. Si usted necesita un "entre dos valores de" probabilidad - es decir, p (a lt; X lt; b) - Realice los pasos 1-4 para b (el mayor de los dos valores) y de nuevo por una (el menor de los dos valores), y restar los resultados.

Al utilizar la aproximación normal para encontrar una probabilidad binomial, su respuesta es un aproximación (no exacta) - asegúrese de indicar eso. También muestran que usted marcó las dos condiciones necesarias para el uso de la aproximación normal.