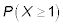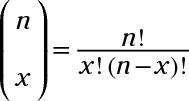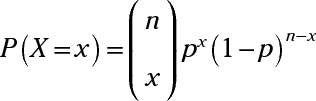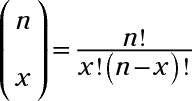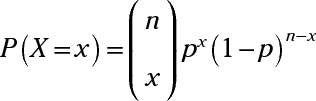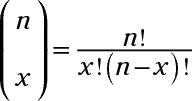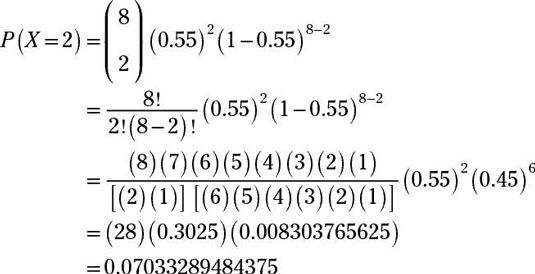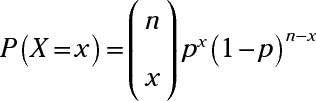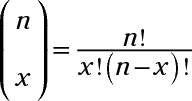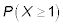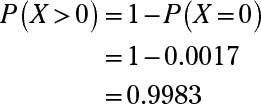Encontrar probabilidades binomiales con una fórmula
Aquí, se llega a practicar la búsqueda de probabilidades binomiales usando una fórmula. Los siguientes problemas tienen una variable aleatoria binomial con p = 0.55. Utilice las siguientes fórmulas para la distribución binomial para los problemas.
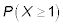
dónde
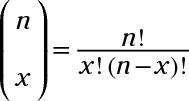
y
n! = (n - 1) (n - 2) (n - 3). . . (3) (2) (1)
Ejemplos de preguntas
¿Cuál es la probabilidad de que exactamente un éxito en ocho ensayos? Redondea tu respuesta a cuatro decimales.
Responder: 0.0164
La fórmula para el cálculo de una probabilidad para una distribución binomial es
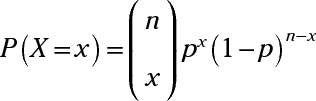
Aquí,
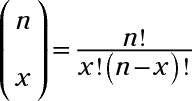
y n! medio n(n - 1) (n - 2). . . (3) (2) (1). Por ejemplo 5! = (5) (4) (3) (2) (1) = 120- 2! = (2) (1) = 1 2-! = 1 y por convención, 0! = 1.
Para encontrar la probabilidad de exactamente un éxito en ocho ensayos, necesita P(X = 1), donde n = 8 (recordar que p = 0.55 aquí):
Redondeado a cuatro decimales, la respuesta es 0.0164.
¿Cuál es la probabilidad de que exactamente dos éxitos en ocho ensayos? Redondea tu respuesta a cuatro decimales.
Responder: 0.0703
La fórmula para el cálculo de una probabilidad para una distribución binomial es
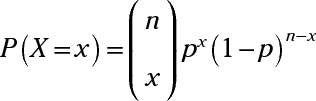
Aquí,
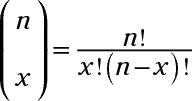
y n! medio n(n - 1) (n - 2). . . (3) (2) (1). Por ejemplo 5! = (5) (4) (3) (2) (1) = 120- 2! = (2) (1) = 1 2-! = 1 y por convención, 0! = 1.
Para encontrar la probabilidad de que exactamente dos éxitos en ocho ensayos, que desea P(X = 2), donde n = 8 (recordar que p = 0.55 aquí):
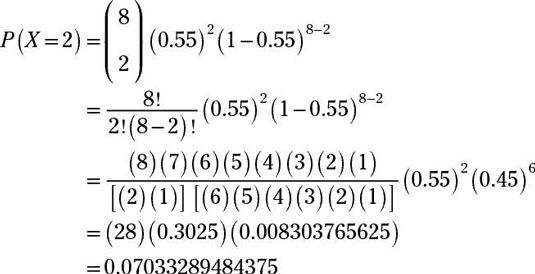
Redondeado a cuatro decimales, la respuesta es 0.0703.
¿Cuál es la probabilidad de obtener al menos un éxito en ocho ensayos? Redondea tu respuesta a cuatro decimales.
Responder: 0.9983
La fórmula para el cálculo de una probabilidad para una distribución binomial es
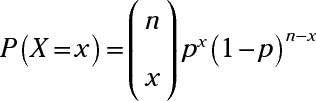
Aquí,
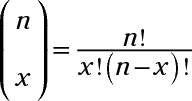
y n! medio n(n - 1) (n - 2). . . (3) (2) (1). Por ejemplo 5! = (5) (4) (3) (2) (1) = 120- 2! = (2) (1) = 1 2-! = 1 y por convención, 0! = 1.
En este caso, X es el número de éxitos en n ensayos. Quieres
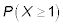
porque "al menos uno" significa lo mismo que "uno o más". La forma más fácil responder a esta pregunta es tomar 1 menos P(X = 0), porque eso es todo lo contrario y más fácil de encontrar.
Redondeado a cuatro decimales, esta respuesta es 0.017. Ahora, conecte el valor de P(X = 0) en la fórmula para encontrar P(X > 0):
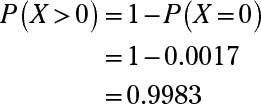
Si necesita más práctica sobre este y otros temas de su curso de estadística, visite 1.001 Estadísticas Entrenamiento Problemas para Dummies comprar acceso en línea a 1.001 problemas de práctica estadísticas! Podemos ayudarle a rastrear su rendimiento, ver dónde se necesita para estudiar y crear un problema personalizado establece para dominar sus habilidades de Estadísticas.
-
¿Cómo encontrar coeficientes binomiales -
La determinación de la media de una variable aleatoria discreta -
Diferenciar entre distribuciones de probabilidad discretas y continuas -
Calcular probabilidades binomiales utilizando la tabla binomial -
Cómo calcular las probabilidades geométricas -
¿Cómo encontrar probabilidades binomiales utilizando una fórmula estadística
¿Cómo encontrar probabilidades estadísticas en una distribución normal Si su muestra estadística tiene una distribución normal (X), Entonces usted puede utilizar el Z-mesa para encontrar la probabilidad de que algo va a ocurrir dentro de un conjunto definido de parámetros. Por ejemplo, usted podría mirar a la…
¿Cómo encontrar la media, la varianza y la desviación estándar de una distribución binomial Debido a que la distribución binomial se utiliza tan comúnmente, los estadísticos se adelantaron e hicieron todo el trabajo sucio de averiguar bonitas fórmulas, fácil de encontrar su media, la varianza y la desviación estándar. Los siguientes…
¿Cómo encontrar los momentos de la distribución binomial Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. El valor esperado representa el valor medio o promedio de una distribución. El valor esperado se conoce a…
¿Cómo encontrar los momentos de la distribución geométrica Momentos son medidas de resumen de una distribución de probabilidad, e incluyen el valor esperado, la varianza y la desviación estándar. Los momentos de la distribución geométrica depende de cuál de las siguientes situaciones se está…
¿Cómo encontrar la aproximación normal a la binomial con una amplia muestra n Si usted está trabajando de una gran muestra estadística, a continuación, la solución de problemas utilizando la distribución binomial puede parecer desalentador. Sin embargo, en realidad hay una manera muy fácil para aproximar la…
Cómo graficar la distribución binomial Una forma de ilustrar la distribución binomial es con un histograma. Un histograma muestra los valores posibles de una distribución de probabilidad como una serie de barras verticales. La altura de cada barra refleja la probabilidad de cada valor…
Cómo identificar una variable aleatoria binomial La variable aleatoria discreta más conocido y amado en las estadísticas es el binomio. Binomial medio dos nombres y se asocia con situaciones que participen dos resultados- por ejemplo, sí / no, o el éxito / fracaso (golpear una luz roja o no,…
Cómo saber cuando una variable aleatoria no tiene una distribución binomial Con el fin de saber cuándo una variable aleatoria de una muestra estadística no tiene una distribución binomial, primero tiene que saber lo que hace que sea binomial. Puede identificar una variable aleatoria binomial como si se cumplen las cuatro…
Cómo utilizar el t-mesa para resolver los problemas de estadística los t-mesa (para el t-distribución) es diferente de la Z-mesa (para el Z-distribución) - asegúrese de entender los valores de la primera y última filas. Encontrar probabilidades para varios t-distribuciones, utilizando el t-mesa, es una valiosa…
Variables aleatorias y distribuciones de probabilidad en las estadísticas empresariales Variables aleatorias y distribuciones de probabilidad son dos de los conceptos más importantes en las estadísticas. LA variable al azar asigna valores numéricos únicos para los resultados de un experimento- azar este es un proceso que genera…
Distribuciones estadísticas: binomial, y t-distribución normal Una distribución estadística es una lista de los posibles valores de una variable (o intervalos de valores) y la frecuencia (o en qué densidad) que se produzcan. Se puede tomar varias formas, incluyendo binomial, normal, y t-distribución.LA…
Apegarse a una estrategia al resolver problemas de estadística Solución de problemas de estadística siempre se trata de tener una estrategia. No se puede leer un problema una y otra vez y esperar para llegar a una respuesta - todo lo que se obtiene es la ansiedad! Aunque no todas las estrategias funcionan…