¿Cómo encontrar coeficientes binomiales
Dependiendo del número de veces que se debe multiplicar el mismo binomio - un valor también conocido como exponente - los coeficientes binomiales para que exponente particular, son siempre los mismos. Los coeficientes binomiales se encuentran utilizando el
fórmula combinaciones. Si el exponente es relativamente pequeño, se puede utilizar un acceso directo llamado Pascal's triángulo encontrar estos coeficientes. Si no, siempre puede confiar en el álgebra!
Pascal's triángulo, llamado así por el famoso matemático Blaise Pascal, nombres de los coeficientes binomiales para la expansión binomial. Es especialmente útil cuando la crianza de un binomial para bajar grados. Por ejemplo, si un maestro sádico le pidió que encontrara (3X + 4)10, es probable que no se desea utilizar de triángulo de Pascal en cambio, usted sólo tiene que utilizar la fórmula algebraica se describe en breve. La figura ilustra este concepto. El número superior del triángulo es 1, así como todos los números en los lados exteriores. Para obtener cualquier término en el triángulo, a encontrar la suma de los dos números por encima de ella.
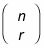
Cada fila da los coeficientes a (la + b)n, empezando con n = 0. Para encontrar los coeficientes binomiales para (la + b)n, utilizar el nª fila y siempre comienzan con el inicio. Por ejemplo, los coeficientes de dos términos de (la + b)5 son 1, 5, 10, 10, 5, y 1 - en ese orden.
Si usted necesita encontrar los coeficientes de binomios algebraicamente, hay una fórmula para eso también. los rº coeficiente para la nª expansión binomial se escribe de la siguiente forma:
Usted puede recordar el término factorial de sus clases de matemáticas anteriores. Si no, aquí es un recordatorio: n!, cuyo texto es el "n factorial", se define como
Usted lee la expresión para el coeficiente binomial
como "n escoger r."Generalmente, usted puede encontrar un botón para combinaciones en una calculadora. Si no es así, puede utilizar el botón factorial y hacer cada parte por separado.
Para hacer las cosas un poco más fácil, 0! se define como 1. Por lo tanto, usted tiene estas igualdades:
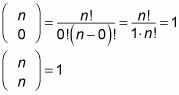
Por ejemplo, para encontrar el coeficiente binomial dada por
sustituir los valores en la fórmula:
Cómo sumar y restar las variables Si agrega o resta variables, seguir la misma regla, a pesar de que tienen diferentes operaciones: Al añadir o restar términos que tienen exactamente las mismas variables, o bien sumar o restar los coeficientes, y dejar que el resultado de pie con…
¿Cómo trabajar con coeficientes Álgebra simplifica expresiones con coeficientes, que son números anteriores variables. Por ejemplo, 3 es el coeficiente en 3X. En lugar de utilizar un signo de multiplicación entre 3 y X, el número se acaba de escribir en frente de una variable,…
Cómo expandir un binomio cuya monomios no tienen coeficientes o exponentes Los resultados finales de una expansión binomial dependen de si el monomio original tenía no hay coeficientes o exponentes (excepto 1) de las variables. Para encontrar la expansión de binomios con el teorema en una situación básica, siga estos…
Cómo expandir un binomio que contiene números complejos El tipo más complicado de la expansión binomial implica el número complejo yo, porque no sólo está tratando con el teorema del binomio, pero se trata de números imaginarios también. Al subir los números complejos a una potencia, tenga en…
Cómo expandir una binomial cuya monomios tienen coeficientes o se elevado a una potencia A veces, monomios pueden tener coeficientes y / o ser elevado a una potencia antes de comenzar la expansión binomial. En este caso, hay que levantar todo el monomio a la potencia adecuada en cada paso. Por ejemplo, así es como se expande la…
¿Cómo adivinar y comprobar raíces reales - 3 - raíces de pruebas por polinomios dividen usando división sintética Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división sintética. División…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…
Cómo escribir un sistema en forma de matriz En un sistema de ecuaciones lineales, donde cada ecuación está en la forma Hacha + Por + Cz + . . . = K, puede representar los coeficientes de este sistema en la matriz, llamada matriz de coeficientes. Si todas las variables se alinean entre sí…
Sistemas de ecuaciones usando determinantes de problemas: la regla de Cramer Si tu profesor de pre-cálculo le pide que resolver un sistema de ecuaciones, puede él o ella impresionar usando la regla de Cramer en lugar de utilizar una calculadora gráfica.La regla de Cramer dice que si el determinante de una matriz de…
Determinar el área de un triángulo a partir de sus tres lados Cuando se conoce la longitud de los tres lados de un triángulo y usted no sabe de altitud, puede utilizar la fórmula de héroe para encontrar el área. Echale un vistazo:dónde la, b, y c son las longitudes de los lados del triángulo y S es el…
Encontrar probabilidades binomiales con una fórmula Aquí, se llega a practicar la búsqueda de probabilidades binomiales usando una fórmula. Los siguientes problemas tienen una variable aleatoria binomial con p = 0.55. Utilice las siguientes fórmulas para la distribución binomial para los…
¿Cómo encontrar probabilidades binomiales utilizando una fórmula estadística Después de identificar que una variable aleatoria X tiene una distribución binomial, es probable que desee encontrar probabilidades para X. La buena noticia es que usted no tiene que encontrarlos a partir del rasguño se llega a utilizar fórmulas…