Matemáticas normas fundamentales comunes: álgebra

Álgebra es el conocimiento esencial para un estudiante de secundaria que intenta cumplir con las normas fundamentales comunes. El álgebra es una rama de las matemáticas que utiliza letras y otros símbolos en las ecuaciones para representar valores desconocidos y luego utiliza lo que se conoce de averiguar lo que es desconocido.

Por ejemplo, si 5X = 40 (es decir, 5 multiplicado por X es igual a 40), usted sabe que X = 8, porque dado lo que han dicho - la información conocida - 5 es el único número que hace que la oración sea verdadera (5 x 8 = 40) número.

Estructura expresiones

Un mayor énfasis es en la interpretación de las partes de una expresión, como coeficientes y términos. En matemáticas, una coeficiente es el lugar número antes de una variable (por lo que en 4X, 4 es el coeficiente y X es la variable). LA término puede ser un solo número, una variable o un coeficiente y variables juntos.

La comprensión de la interacción de los coeficientes y variables resultados en los estudiantes sean capaces de reescribir la expresión de diferentes maneras, lo que requiere una comprensión de cada parte de la expresión y de cómo todas las partes de una expresión interactúan dadas las reglas de operaciones matemáticas.

Expresiones son números, símbolos y operadores (+, -, x, y # 247-) agrupados para mostrar valor. Expresiones difieren de ecuaciones, que emplean el uso de un signo igual (=) para mostrar que los valores a cada lado de ella son iguales o para demostrar el valor de una variable.

Práctica traducir escrito o hablado expresiones en expresiones numéricas para su uso en los cálculos. Por ejemplo, puede escribir la declaración " 2 menos de 5 veces al número " como la expresión 5x - 2. Si X = 7, a continuación, 5 (7) - 2 = 35 - 33 = 2.

Polinomios y expresiones racionales

Los estudiantes comienzan a trabajar con polinomios, que son expresiones que tienen más de una variable. Utilizan suma, resta, multiplicación y división con polinomios.

Los estudiantes también son introducidos al concepto de factoring para simplificar expresiones y resolver problemas. Factoring implica valores encontrando que multiplicado juntos dan como resultado la expresión: por ejemplo, la expresión 5X - 5 se puede factorizar como 5 (X - 1) de la misma manera que 14 se puede factorizar como 2 x 7.

Escriba un polinomio y que su hijo nombrar las partes, como en el siguiente ejemplo:

4X2 + 5X - 3

Esto es un trinomio porque tiene tres expresiones unidas entre sí con los operadores. Es fácil confundirse y contar el X y x2 como entidades separadas, pero en este problema que son parte de los coeficientes al lado de ellos. Los operadores (suma y resta señales en este problema) se separan las partes de este trinomio.

El número 4 es el Coeficiente de liderazgo, X es un variable, 2 es una exponente, y 2 es también el más alto poder en la ecuación. El 2 al final es una constante.

Resolver este problema, lo que implica un polinomio: Si el área de un rectángulo se expresa como X2 + 7X + 12 y la longitud de un lado es X + 4, ¿cuál es la longitud del otro lado?

Para resolver este problema, el factor X2 + 7X + 12 como (X + 3) (X + 4), por lo que la longitud del otro lado es (x + 3).

Ecuaciones

Los estudiantes utilizan ecuaciones para describir las relaciones que existen entre las variables, incluyendo la resolución de ecuaciones que son representativos de situaciones del mundo real. El uso de modelado (la aplicación de los conceptos matemáticos a situaciones prácticas) es un aspecto importante de estas normas.

Las relaciones entre las variables implican la interacción entre las variables y coeficientes. Por ejemplo, en 3X = y, El valor de y es dependiente del valor de X. En otras palabras, como el valor de X aumenta o disminuye, también lo hace el valor de y.

Construye una ecuación para resolver un problema que involucra un escenario del mundo real. Por ejemplo, imagine que un agricultor quiere construir un corral rectangular para sus animales. Tiene 200 pies de materiales de esgrima, y ​​necesita un lado del rectángulo a ser de 30 pies de largo. ¿Cuánto tiempo las otras partes tienen que ser?

Comience por dibujar un rectángulo y el etiquetado de los dos lados más cortos " 30 pies ". Etiquetar los dos lados más largos "X."

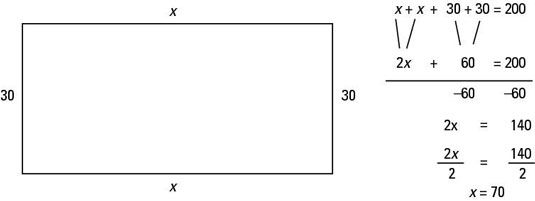
Representado en la forma de una ecuación, se escribe: X + X + 30 + 30 = 200. Después de combinar los términos semejantes, uno se queda con 2X + 60 = 200. Resta 60 de ambos lados de la ecuación, y se obtiene 2X = 140. Divide ambos lados por 2, y usted tiene su respuesta: Cada uno de los lados más largos del rectángulo es de 70 pies.

Razón con ecuaciones y desigualdades

Los estudiantes resuelven ecuaciones mediante la búsqueda de soluciones precisas, la práctica de la habilidad de sustituir los números de las variables para asegurar la precisión. Comprobación de la exactitud de una respuesta, incluida la forma razonable una respuesta es en el contexto de un problema, hace más para desarrollar habilidades de resolución de problemas que simplemente tener un estudiante utiliza un algoritmo para resolver ecuaciones. Un algoritmo es un procedimiento paso a paso para resolver un problema.

Comprobación de exactitud respuesta es una habilidad esencial. Cuando la solución para una variable en una ecuación, como por ejemplo 3X + 5 = 35, los estudiantes pueden enchufar en su respuesta para X para ver si tienen razón. Así que después de la resolución de X y encontrar que X es igual a 10, que se conectan en el 10 por X y hacer los cálculos: 3 (10) + 5 = 35. Si ambos lados son iguales, el problema es la correcta.

Verificación de la razonabilidad de la respuesta consiste en hacer una determinación lógica de si la respuesta es razonable teniendo en cuenta el contexto de un problema de matemáticas. Por ejemplo, si un objeto es lanzado hacia arriba en el aire, ¿cuánto tiempo se necesita para que el objeto a golpear el suelo, teniendo en cuenta que s(t) = t2 - 2t + 35, con t que representa el tiempo medido en segundos?

Por lo tanto, t puede ser igual a -7 segundos o 5 segundos. Es -7 segundos una respuesta razonable? ¡Por supuesto que no!