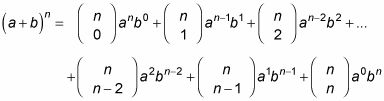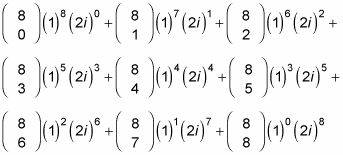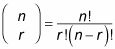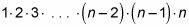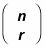Cómo expandir un binomio que contiene números complejos
El tipo más complicado de la expansión binomial implica el número complejo yo, porque no sólo está tratando con el teorema del binomio, pero se trata de números imaginarios también. Al subir los números complejos a una potencia, tenga en cuenta que yo1 = I, yo2 = -1, yo3 = -yo, y yo4 = 1. Si se encuentra con poderes superiores, este patrón se repite: yo5 = yo, yo6 = -1, yo7 = -yo, etcétera. Debido poderes del número imaginario yo se puede simplificar, su respuesta final a la expansión no debe incluir poderes de yo. En su lugar, utilice la información dada aquí para simplificar los poderes de yo y luego combine los términos semejantes.
Por ejemplo, para ampliar (1 + 2yo)8, sigue estos pasos:
Escriba la expansión binomial utilizando el teorema del binomio, sustituyendo en las variables cuando sea necesario.
En caso de haber perdido, aquí está el teorema del binomio:
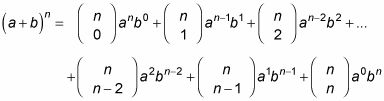
Usando el teorema, (2 + 1yo)8 expande para
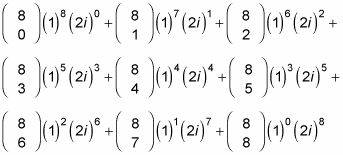
Encuentra los coeficientes binomiales.
Para ello, se utiliza la fórmula para la expansión binomial, que está escrito en la forma siguiente:
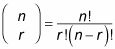
Usted puede recordar el término factorial de sus clases de matemáticas anteriores. Si no, aquí es un recordatorio: n!, cuyo texto es el "n factorial", se define como
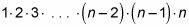
Utilizando la fórmula de combinación que da la siguiente:
Reemplaza todo
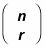
con los coeficientes de la Etapa 2.
1 (1)8(2yo)0 + 8 (1)7(2yo)1 + 28 (1)6(2yo)2 + 56 (1)5(2yo)3 + 70 (1)4(2yo)4 + 56 (1)3(2yo)5 + 28 (1)2(2yo)6 + 8 (1)1(2yo)7 + 1 (1)0(2yo)8
Levante los monomios a los poderes especificados para cada término.
1 (1) (1) + 8 (1) (2i) + 28 (1) (4I2) + 56 (1) (8i3) + 70 (1) (16i4) + 56 (1) (32i5) + 28 ( 1) (64i6) + 8 (1) (128i7) + 1 (1) (256i8)
Simplifique cualquier yo's que se puede.
1 (1) (1) + 8 (1) (2i) + 28 (1) (4) (- 1) + 56 (1) (8) (- i) + 70 (1) (16) (1) + 56 (1) (32) (i) + 28 (1) (64) (- 1) + 8 (1) (128) (- i) + 1 (1) (256) (1)
Combine los términos semejantes y simplificar.
1 + 16i - 112 - 448i + 1120 + 1,792i - 1792 - 1,024i + 256
= -527 + 336i
-
Cómo utilizar el teorema del binomio en la TI-84 Plus -
¿Cómo trabajar con números complejos en la TI-84 Plus -
Matemáticas normas fundamentales comunes: el sistema de números complejos -
10 Errores a evitar al trabajar con exponentes -
Álgebra II: elevar binomios a una potencia -
Álgebra II: ¿cuál es el teorema del binomio?
Álgebra II libro para los maniquíes Los exponentes son la abreviatura para la multiplicación repetida. Las reglas para las operaciones que involucran exponentes realizar permiten cambiar las expresiones de multiplicación y división con la misma base en algo más sencillo trabajar…
Las variables que se dividen en álgebra La división de las variables en un problema de álgebra es bastante sencillo. Cada variable se considera por separado. Los coeficientes de números se reducen los mismos que en fracciones simples. Al dividir las variables, se escribe el problema…
Cómo sumar y restar con poderes Para agregar o restar con poderes, tanto las variables y los exponentes de las variables debe ser el mismo. Realizar las operaciones necesarias en los coeficientes, dejando la variable y el exponente como son. Al añadir o restar con poderes, los…
Cómo distribuir binomios Cuando distribuye en álgebra, se multiplica cada uno de los términos dentro del paréntesis por otro término que se encuentra fuera de los paréntesis. Así que, cuando distribuya un binomio largo de varios términos, que acaba de aplicar el…
Cómo distribuir un polinomio La distribución de un polinomio no es difícil. Cuando la distribución de un polinomio sobre cualquier número de otros términos, se distribuye cada término en el primer factor sobre la totalidad de los términos en el segundo factor. Cuando se…
¿Cómo reconocer un binomio perfectamente cuadrado Reconociendo un binomio perfectamente cuadrado puede hacer la vida más fácil. Cuando reconoces perfectamente cuadrado binomial, que haya identificado un atajo que ahorra tiempo al distribuir binomios sobre otros términos.Cuando el mismo binomio…
Cómo simplificar expresiones factoriales Conjuntos de elementos tienen operaciones especiales utilizados para combinarlos o cambiarlos. Otra operación que se utiliza con conjuntos (pero que no es exclusivo de juegos) es factorial, denotado por el signo de exclamación.Utilice la…
Los números complejos en pre-cálculo Los números complejos son irreales. Sí, esa es la verdad. Un número complejo tiene un término con un múltiplo de yo, y yo es el número imaginario igual a la raíz cuadrada de -1. Muchas de las reglas algebraicas que se aplican a los números…
Cómo romper una diferencia cúbica o la suma Después de que se haya registrado para ver si hay un máximo común divisor (MCD) de un polinomio dado y descubrió que es un binomio que no es una diferencia de cuadrados, se debe considerar que puede ser una diferencia o suma de cubos.LA…
Cómo expandir un binomio cuya monomios no tienen coeficientes o exponentes Los resultados finales de una expansión binomial dependen de si el monomio original tenía no hay coeficientes o exponentes (excepto 1) de las variables. Para encontrar la expansión de binomios con el teorema en una situación básica, siga estos…
Cómo expandir una binomial cuya monomios tienen coeficientes o se elevado a una potencia A veces, monomios pueden tener coeficientes y / o ser elevado a una potencia antes de comenzar la expansión binomial. En este caso, hay que levantar todo el monomio a la potencia adecuada en cada paso. Por ejemplo, así es como se expande la…
¿Cómo encontrar coeficientes binomiales Dependiendo del número de veces que se debe multiplicar el mismo binomio - un valor también conocido como exponente - los coeficientes binomiales para que exponente particular, son siempre los mismos. Los coeficientes binomiales se encuentran…