Matemáticas normas fundamentales comunes: el sistema de números complejos
Los estudiantes de secundaria tendrán que saber sobre el sistema de números complejos de Estándares Básicos Comunes. los sistema de números complejos incluye tanto los números reales e imaginarios. Un número imaginario, representado como yo, es la raíz cuadrada de 1- yo es imaginario porque no hay ningún número multiplicado por sí mismo da como resultado un valor negativo.
En el grado 11, los estudiantes encuentran los números imaginarios como traducción en el plano imaginario. Esto es lo que los estudiantes deben saber y ser capaces de hacer cuando se trata del sistema de números complejos:
Explique lo que es un número complejo (imaginario) es:
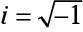
o
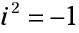
la + bi = Un número complejo, con tanto la y b siendo los números reales
Sumar, restar y multiplicar números complejos utilizando el conmutativa, asociativa y distributiva:
Conmutativa le permite agregar o multiplicar números en cualquier orden, por ejemplo 4 + 2 = 2 + 4
De asociación significa que puede agregar o multiplicar números en cualquier agrupación, por ejemplo (3 x 5) x 4 = 3 x (5 x 4)
Distribución se representa comúnmente como
una x (b + c) = (A x B) + (una x c)
Así, los estudiantes deben ser capaces de resolver ecuaciones, tales como:
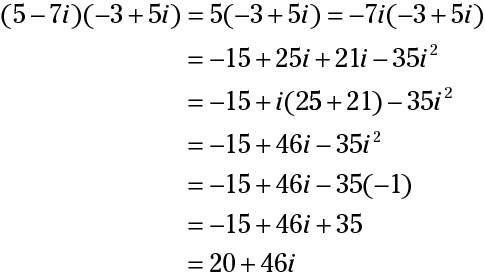
Encontrar el conjugado de un número complejo y el uso de los conjugados para encontrar módulos y cocientes de números complejos. LA conjugado es un expresión binomial (que representa la suma o diferencia de dos términos) formado por negar el segundo término de un binomial- por ejemplo, el conjugado de a + b es a - b.
Cuando un número imaginario es participar, usted tiene un complejo conjugado- por ejemplo, en la expresión m = la + bi el conjugado complejo representado es:
Un problema muestra puede proporcionar un hecho y pedirle que utilice el conjugado para encontrar el módulo y quotient- por ejemplo, teniendo en cuenta que y = 3 - 7 deyo y z = 5 + 2yo, encontrar el módulo de y y el cociente de z y y:
Para encontrar el módulo de y utilizando su complejo conjugado, los estudiantes pueden resolver una ecuación como la siguiente:
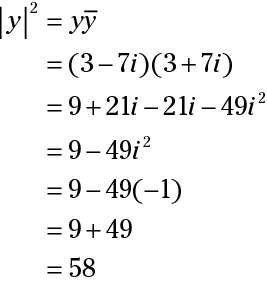
o
Como se puede ver, se utiliza la propiedad distributiva para multiplicar los dos binomios en el primer paso. Usted puede utilizar el método FOIL (primeros términos, condiciones externas, términos, dentro últimos términos) para recordar cómo hacer esto: primero (3 x 3), exterior (3 x 7yo), En el interior (-7yo x 3), y la última (-7yo x 7yo). Después de la multiplicación de estos términos, se llega a un polinomio con cuatro términos.
Entonces usted combina los términos semejantes y completar todas las operaciones restantes. Porque yo es la raíz cuadrada de -1, puede cambiar yo2 en -1 y se multiplica por -49, lo que resulta en el cambio a un número positivo. Después de calcular 9 + 49 = 58, tomar la raíz cuadrada de 58 porque usted está resolviendo para y2 y desee encontrar y en su lugar.
Para encontrar el cociente de z y y:
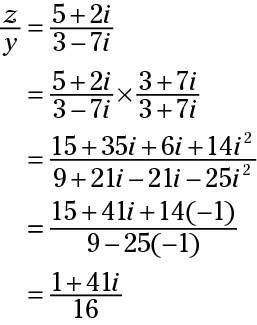
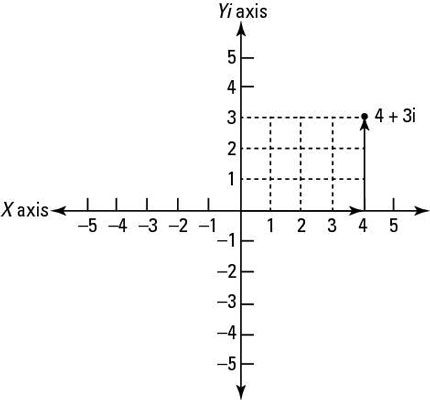
Representar los números complejos en el plano complejo en forma rectangular y polar y explicar por qué las formas rectangulares y polares de un número complejo representan el mismo número. En el plano complejo, el eje horizontal (X # 8201-) Representa números reales, y el eje vertical (Yi) Representa los números imaginarios. Los números imaginarios se pueden representar en el plano complejo en dos formas:
Forma rectangular: La intersección de los números reales e imaginarias se muestra como la intersección de las coordenadas en la X y Yi ejes.
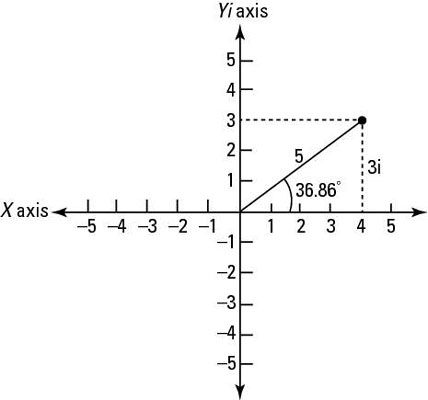
Forma polar: El número real representa la longitud del vector (hasta qué punto el vector alcanza en el plano imaginario), y # 952- representa el ángulo de las formas de vector con el eje real (el eje familiarizado representado por X y y). Polar forma se deriva de la teorema de Pitágoras, r2 = la2 + b2.
Representar a la suma, resta, multiplicación, y la conjugación en el plano complejo.
Resolver ecuaciones cuadráticas (ecuaciones en las que la mayor potencia de un desconocido es un cuadrado) con coeficientes reales que tienen soluciones complejas. Por ejemplo, los estudiantes se les puede pedir para resolver X2 + 2X = Números 0 sobre complejas.
Extender identidades polinómicas a los números complejos. Por ejemplo, X + 7 usando números complejos puede expresarse como (X + 7yo) X (X - 7yo).
Sujete la Teorema fundamental del álgebra, que establece que cualquier polinomio de n grado tiene n raíces (lugares donde el polinomio es igual a cero cuando grafican). Por ejemplo, en un polinomio con una variable, tales como 5x6 + 8x - 2, la n grado es 6, por lo que el polinomio tiene 6 raíces.
Usted puede apoyar a su hijo en casa, mostrando monitoreo interesante progreso- alentar a su hijo a buscar ayuda, si es necesario- y expresar cualquier inquietud que tenga a profesor de matemáticas de su hijo. También puede localizar a los sitios web que pueden ayudar a entender estos conceptos, como Khan Academy o ilustrativos Matemáticas.




