Cómo realizar operaciones con números complejos

A veces te encuentras con situaciones en las que debe operar en números reales e imaginarios en conjunto, por lo que desea escribir tanto números como números complejos con el fin de ser capaz de sumar, restar, multiplicar o dividir ellos.

Considere los siguientes tres tipos de números complejos:

• Un número real como un número complejo: 3 + 0yo

  Observe que la parte imaginaria de la expresión es 0.

• Un número imaginario como un número complejo: 0 + 2yo

  Observe que la parte real de la expresión es 0.

• Un número complejo tanto con una real y una parte imaginaria: 1 + 4yo

  Este número no puede ser descrito como el único real o imaginario exclusivamente - de ahí el término compleja.

Puede manipular los números complejos aritméticamente al igual que los números reales para llevar a cabo las operaciones. Sólo tienes que tener cuidado de mantener toda la yo's recta. No es posible combinar las piezas reales con partes imaginarias mediante adición o sustracción, porque no son como los términos, así que hay que mantenerlos separados. Además, cuando la multiplicación de números complejos, el producto de dos números imaginarios es un número- real, el producto de una real y un número imaginario es todavía imaginario- y el producto de dos números reales es real. Muchas personas se confunden con este tema.

La siguiente lista presenta las posibles operaciones con números complejos.

• Para sumar y restar números complejos: Simplemente combine términos semejantes. Por ejemplo, (3 - 2yo) - (2 - 6yo) = 3 - 2yo - 2 + 6yo = 1 + 4yo.

• Para multiplicar cuando está involucrado un número complejo, utilizar uno de tres métodos diferentes, basados ​​en la situación:

• Para multiplicar un número complejo por un número real: Sólo distribuir el número real tanto a la parte real e imaginaria del número complejo. Por ejemplo, aquí es cómo usted maneja un escalar (una constante) multiplicar un número complejo en paréntesis: 2 (3 + 2yo) = 6 + 4yo.

• Para multiplicar un número complejo por un número imaginario: En primer lugar, darse cuenta de que la parte real del número complejo se convierte en imaginario y que la parte imaginaria se convierte en real. Al expresar su respuesta final, sin embargo, todavía se expresa la parte real primero seguido de la parte imaginaria, en la forma A + Byo.

  Por ejemplo, así es como 2yo se multiplica en el mismo número entre paréntesis: 2yo(3 + 2yo) = 6yo + 4yo². Nota: Usted define yo como

  

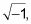
  así que eso yo² = -1! Por lo tanto, usted realmente tiene 6yo + 4 (-1), por lo que su respuesta se hace -4 + 6yo.

• Para multiplicar dos números complejos: Simplemente siga el proceso FOIL (Primera, externos, internos, Apellido). Por ejemplo, (3 - 2yo) (9 + 4yo) = 27 + 12yo - 18yo - 8yo², que es el mismo que 27-6yo - 8 (-1), o el 35 - 6yo.

Por ejemplo, digamos que se le pide que dividir

El conjugado complejo de 3 - 4yo es 3 + 4yo. Siga estos pasos para terminar el problema:

1. Multiplica el numerador y el denominador por el conjugado.

   

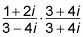
2. Frustrar el numerador.

   Vas con (1 + 2yo) (3 + 4yo) = 3 + 4yo + 6yo + 8yo², lo que simplifica a (3 - 8) + (4yo + 6yo), O -5 + 10yo.

3. Frustrar el denominador.

   Usted tiene (3 - 4yo) (3 + 4yo), Que las láminas de 9 + 12yo - 12yo - 16yo². Porque yo² = -1 Y 12yo - 12yo = 0, uno se queda con el verdadero número 9 + 16 = 25 en el denominador (por eso se multiplica por 3 + 4yo en primer lugar).

4. Vuelva a escribir el numerador y el denominador.

   

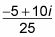
   Esta respuesta todavía no está en la forma correcta para un número complejo, sin embargo.

5. Separar y dividir las dos partes por el denominador constante.

   

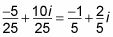
   Observe que la respuesta es, finalmente, en la forma A + Byo.