Cómo racionalizar un radical de un denominador
Una convención de las matemáticas es que usted no deja radicales en el denominador de una expresión cuando se escribe en su forma final. Así que hacemos algo que se llama racionalizar el denominador.
Conteúdo
Un numerador puede contener un radical, pero el denominador no puede. La expresión final puede parecer más complicado en su forma racional, pero eso es lo que tiene que hacer a veces.
Hay dos situaciones distintas en que los radicales pueden aparecer en el denominador de una fracción: en que las expresiones contienen un radical en el denominador, y donde las expresiones contienen dos términos en el denominador, al menos uno de los cuales es un radical.
Racionalizar con un radical en el denominador
Racionalizar expresiones con un radical en el denominador es fácil. Por ejemplo, con una raíz cuadrada, sólo tiene que deshacerse de la raíz cuadrada. Normalmente, la mejor manera de hacerlo que en una ecuación es la cuadratura ambos lados. Por ejemplo,
Sin embargo, no se puede caer en la trampa de la racionalización de una fracción de la cuadratura del numerador y el denominador. Por ejemplo, la cuadratura de la parte superior e inferior de
En lugar de ello, siga estos pasos:
Multiplica el numerador y el denominador por la misma raíz cuadrada.
Hagas lo que multiplica a la parte inferior de una fracción, debe multiplicar a las láminas superior de esta manera, es realmente como que multiplicado por uno y que no cambia la fracción. Esto es lo que parece:
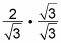
Multiplique las copas y multiplicar los fondos y simplificar.
Para este ejemplo, se obtiene
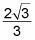
El proceso para la racionalización de una raíz cúbica en el denominador es bastante similar a la de racionalizar una raíz cuadrada. Para deshacerse de una raíz cúbica en el denominador de una fracción, debe cubicar ella. Si el denominador es una raíz cúbica a la primera potencia, por ejemplo, se multiplica el numerador y el denominador por la raíz cúbica a la segunda potencia para obtener la raíz cúbica a la tercera potencia (en el denominador). Criar a un raíz cúbica a la tercera potencia cancela la raíz - y ya está!
La racionalización cuando el denominador es una binomial con al menos un radical
Debe racionalizar el denominador de una fracción cuando contiene un binomio con un radical. Por ejemplo, mira las siguientes ecuaciones:
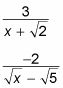
Deshacerse del radical en estos denominadores implica el uso del conjugado de los denominadores. LA conjugado es un binomio formado por tomar el opuesto del segundo término del binomio originales. El conjugado de
El conjugado de X + 2 es X - 2- manera similar, el conjugado de
Multiplicar un número por su conjugado es realmente el método FOIL disfrazada. Recuerde del álgebra que FOIL significa primero, exterior, interior, y durar.
Los dos términos medios siempre se anulan entre sí, y los radicales desaparecen. Para este problema, se obtiene X2 - 2.
Echa un vistazo a un ejemplo típico que implica la racionalización de un denominador utilizando el conjugado. En primer lugar, simplificar esta expresión:
Para racionalizar este denominador, se multiplica el arriba y abajo por el conjugado de la misma, que es
El desglose paso a paso cuando haces esta multiplicación es
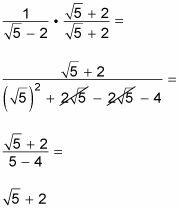
He aquí un segundo ejemplo: Supongamos que usted necesita para simplificar el siguiente problema:
Sigue estos pasos:
Multiplique por el conjugado.
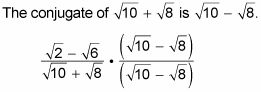
Multiplica los numeradores y denominadores.
Frustrar la parte superior y la parte inferior. (Tricky!) He aquí cómo hacerlo:
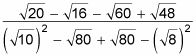
Simplifique.
Tanto el numerador y el denominador simplifican primero
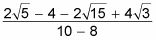
que se convierte
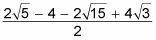
Esta expresión se simplifica aún más debido a que el denominador se divide en cada término en el numerador, que le da
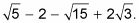
Simplifique cualquier radical en su respuesta final - siempre. Por ejemplo, para simplificar una raíz cuadrada, encontrar factores de raíz cuadrada perfectos:
Además, se puede sumar y restar solamente radicales que son términos semejantes. Esto significa que el número dentro de la radical y la índice (que es lo que te dice si es una raíz cuadrada, una raíz cúbica, un cuarto de la raíz, o lo que sea) son los mismos.
-
Cómo cambiar fracciones impropias a números mixtos -
Cómo crear fracciones equivalentes utilizando denominadores comunes -
¿Cómo resolver problemas de álgebra con símbolos de agrupación -
Trabajar con ecuaciones radicales y racionales en álgebra ii - Consejos de matemáticas básicas: fracciones
-
¿Cómo aumentar los términos de una fracción
Cómo multiplicar dos fracciones y reducir la respuesta Para multiplicar dos fracciones, es necesario tener un conocimiento básico de las tablas de multiplicar y la capacidad de reducir la respuesta a su mínima expresión.Multiplica los numeradores (los números en la parte superior) en conjunto para…
Cómo multiplicar fracciones ¿Por qué no todo en la vida ser tan fácil como la multiplicación de fracciones? Para multiplicar dos fracciones, simplemente hacer lo siguiente: Multiplique los dos numeradores (números superiores) para obtener el numerador de la respuesta-…
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
La comparación de los radicales y exponentes Radicales y exponentes (también conocido como raíces y poderes) Son dos comunes - elementos de álgebra básica - y muchas veces frustrantes. Y por supuesto te siguen donde quiera que vaya en matemáticas, al igual que una nube de mosquitos sigue…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo encontrar el límite de una función algebraica Cuando su profesor de pre-cálculo le pide que encontrar el límite de una función algebraica, usted tiene cuatro técnicas para elegir: enchufar el X valor, el factoring, racionalizar el numerador, y encontrar el mínimo común denominador.El…
Cómo realizar operaciones con números complejos A veces te encuentras con situaciones en las que debe operar en números reales e imaginarios en conjunto, por lo que desea escribir tanto números como números complejos con el fin de ser capaz de sumar, restar, multiplicar o dividir…
Cómo reescribir radicales como exponentes Cuando se te da un problema en forma radical, puede ser más fácil si usted reescribir mediante el uso de exponentes racionales - exponentes que son fracciones. Puede volver a escribir cada radical como un exponente mediante el uso de la siguiente…
Cómo simplificar expresiones trigonométricas con un binomio en el denominador de una fracción Cuando una expresión trigonométrica es una fracción con un binomio en su denominador, siempre tenga en cuenta multiplicando por el conjugado antes de hacer cualquier otra cosa. La mayoría de las veces, esta técnica permite simplificar.Por…
¿Cómo resolver los límites de la multiplicación conjugada Para resolver ciertos problemas de límite, tendrá la técnica de multiplicación conjugado. Cuando la sustitución no funciona en la función original - por lo general a causa de un agujero en la función - se puede usar la multiplicación…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Cómo multiplicar por un conjugado de encontrar una identidad trigonometría Conjugados ofrecen una gran manera de encontrar identidades trigonométricas. En matemáticas, un conjugado formado por los mismos dos términos como la primera expresión, separados por el signo opuesto. Por ejemplo, el conjugado deEn trig,…