Cómo reescribir radicales como exponentes
Cuando se te da un problema en forma radical, puede ser más fácil si usted reescribir mediante el uso de exponentes racionales - exponentes que son fracciones. Puede volver a escribir cada radical como un exponente mediante el uso de la siguiente propiedad - el número superior en el exponente racional resultante le indica el poder, y el número de abajo te dice la raíz que está tomando:
Por ejemplo, se puede reescribir
como
Exponentes fraccionarios son raíces y nada más. Por ejemplo, 6403.01 no significa 64-3 o
En este ejemplo, se encuentra la raíz se muestra en el denominador (la raíz cúbica) y luego la lleva al poder en el numerador (la primera potencia). Así que 6403.01 = 4.
El orden de estos procesos en realidad no importa. Usted puede elegir cualquiera de los métodos:
Raíz cúbica del ese producto 8 y luego cuadrado
Cuadrar la raíz 8 y luego cubo de ese producto
De cualquier manera, la ecuación se simplifica a 4. En función de la expresión original, sin embargo, es posible que el problema más fácil si se toma la raíz primera y luego tomar el poder, o es posible que desee tomar el poder por primera vez. Por ejemplo, 642.3 es más fácil si usted escribe como (642.1)3 = 83 = 512 en lugar de (643)2.1, porque entonces usted tendría que encontrar la raíz cuadrada de 262144.
Echa un vistazo a algunos pasos que ilustran este proceso. Para simplificar la expresión
en lugar de trabajar con las raíces, ejecutar lo siguiente:
Vuelva a escribir la expresión completa usando exponentes racionales.
Ahora usted tiene todas las propiedades de los exponentes disponibles para ayudar a simplificar la expresión: X2.1(X2.3 - X4/3).
Distribuir a deshacerse de los paréntesis.
Al multiplicar monomios con la misma base, se agregan los exponentes.
Por lo tanto, el exponente en el primer término es
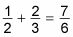
y el exponente del segundo término es 1/2 + 4/3 = 11/6. Para que pueda obtener X7/6 - X6.11.
Debido a que la solución se escribe en forma exponencial y no en forma radical, como la expresión original, reescribirla para que coincida con la expresión original.
Esto le da
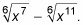
Por lo general, su respuesta final debe estar en el mismo formato que el de problemas original si el problema original está en forma radical, su respuesta debe ser en forma radical. Y si el problema original está en forma exponencial con exponentes racionales, su solución debe ser así.
Cómo distribuir las variables La distribución de las variables en los términos en una expresión algebraica implica reglas de multiplicación y las reglas de los exponentes. Cuando diferentes variables se multiplican entre sí, puede escribir al lado del otro sin necesidad de…
Cómo multiplicar exponentes Usted puede multiplicar muchas expresiones exponenciales juntos sin tener que cambiar su forma en los números grandes o pequeños que representan. Al multiplicar exponentes, el único requisito es que las bases de las expresiones exponenciales…
Cómo aumentar los poderes de poderes Al elevar una potencia a una potencia en una expresión exponencial, se encuentra el nuevo poder de multiplicar los dos poderes juntos. Por ejemplo, en la siguiente expresión, X a la potencia de 3 está siendo elevado a la potencia de 6, y así…
¿Cómo simplificar exponentes negativos con variables Distribuir con exponentes negativos significa que tendrás respuestas fraccionarias. Una base que tiene un exponente negativo se puede cambiar a una fracción. La base y el exponente se convierten en el denominador, pero el exponente pierde su signo…
Las 10 mejores maneras de evitar las trampas de álgebra El gran número de personas que utilizan el álgebra significa que un gran número de errores son inevitables. Tanto el álgebra se hace en el mundo: Casi todo el mundo que avanza más allá de la escuela primaria tiene una clase de álgebra.…
Trabajar con exponentes negativos Exponentes negativos son una forma de escribir poderes de fracciones o decimales sin usar una fracción o decimal. Utiliza exponentes negativos como una manera de combinar expresiones con la misma base, si los diferentes factores están en el…
Trabajar con ecuaciones radicales y racionales en álgebra ii LA radical la ecuación es una que comienza con una raíz cuadrada, raíz cúbica, o alguna otra raíz y se cambia a otra forma para hacer que el proceso de resolución más fácil. LA racional la ecuación es aquella que implica una expresión…
Encuentra la raíz cuadrada de un número A raíz cuadrada es la operación de la raíz más común. A raíz es la operación inversa de un exponente (lo que significa que deshace una operación exponencial), y por lo que una raíz cuadrada es una operación que deshace un exponente de 2.…
La comparación de los radicales y exponentes Radicales y exponentes (también conocido como raíces y poderes) Son dos comunes - elementos de álgebra básica - y muchas veces frustrantes. Y por supuesto te siguen donde quiera que vaya en matemáticas, al igual que una nube de mosquitos sigue…
Cómo racionalizar un radical de un denominador Una convención de las matemáticas es que usted no deja radicales en el denominador de una expresión cuando se escribe en su forma final. Así que hacemos algo que se llama racionalizar el denominador. Esta convención hace que la recogida como…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
ASVAB Preparación: exponentes y notación científica Muchos de los problemas que se ven en las subpruebas de matemáticas ASVAB requieren que usted realice cálculos que involucran exponentes y notación científica. Si esto suena confuso, no preocupe, no es realmente. Siga leyendo.Consejos sobre los…