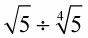Combinando raíces cuadradas
Las raíces cuadradas, que utilizan el símbolo radical, son operaciones no binarios - operaciones que impliquen un solo número - que le piden, "? ¡Qué tiempos número en sí le da este número bajo el radical " Encontrar raíces cuadradas es una operación relativamente común en álgebra, pero trabajar con y combinando las raíces no siempre es tan clara.
Expresiones con radicales pueden ser multiplicadas o divididas, siempre y cuando la potencia de la raíz o el valor bajo el radical es el mismo. Expresiones con radicales no pueden sumarse o restarse a menos que tanto el poder de la raíz y el valor bajo el radical son los mismos.
Cuando encuentre raíces cuadradas, el símbolo de esa operación se llama un radical. El poder de la raíz se refiere al número exterior y la parte superior izquierda del radical. Si no hay un número, se asume que el poder de la raíz es 2.
Cuando se trata de la combinación de los radicales, hay un par de reglas simples para recordar:
Adición y sustracción se puede realizar si la fuente de la raíz y el valor bajo el radical son los mismos.
Ejemplos:
Estos radicales no se pueden combinar porque la operación es adición, y el valor bajo el radical no es el mismo:
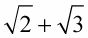
Estos radicales se pueden combinar porque la potencia de la raíz y los números bajo el radical son los mismos:
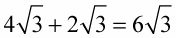
Estos radicales no se pueden combinar porque la operación es la resta, y el poder de la raíz no es el mismo:
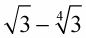
Multiplicación y división se puede realizar si los poderes de raíz son los mismos.
Ejemplos:
Estos radicales se pueden combinar porque la operación es la multiplicación, y el poder de la raíz es la misma:
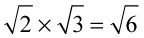
Estos radicales se pueden combinar porque la operación de división, y el poder de la raíz es la misma:
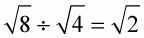
Estos radicales no se pueden combinar porque la operación de división, y el poder de la raíz no es el mismo:
Orden de las operaciones de álgebra Al crear expresiones más sencillas y útiles, que desee tener cuidado de no cambiar el valor original. Mediante la aplicación de la orden de las operaciones, a mantener ese valor.Aplicar el orden de operaciones cuando no hay símbolos de…
Las 10 mejores maneras de evitar las trampas de álgebra El gran número de personas que utilizan el álgebra significa que un gran número de errores son inevitables. Tanto el álgebra se hace en el mundo: Casi todo el mundo que avanza más allá de la escuela primaria tiene una clase de álgebra.…
Trabajar con ecuaciones radicales y racionales en álgebra ii LA radical la ecuación es una que comienza con una raíz cuadrada, raíz cúbica, o alguna otra raíz y se cambia a otra forma para hacer que el proceso de resolución más fácil. LA racional la ecuación es aquella que implica una expresión…
Comprobación de la divisibilidad añadiendo dígitos A veces se puede comprobar la divisibilidad sumando todos o algunos de los dígitos de un número. La suma de los dígitos de un número se llama su raíz digital. Encontrar la raíz digital de un número es fácil, y es muy útil saber.Para…
Encuentra la raíz cuadrada de un número A raíz cuadrada es la operación de la raíz más común. A raíz es la operación inversa de un exponente (lo que significa que deshace una operación exponencial), y por lo que una raíz cuadrada es una operación que deshace un exponente de 2.…
Los paréntesis y potestades en el orden de las operaciones Cuando una expresión tiene paréntesis y poderes, evaluarla en el orden siguiente: contenido de paréntesis, poderes de izquierda a derecha, multiplicación y división de izquierda a derecha, y suma y resta de izquierda a derecha.Contenido de…
La comparación de los radicales y exponentes Radicales y exponentes (también conocido como raíces y poderes) Son dos comunes - elementos de álgebra básica - y muchas veces frustrantes. Y por supuesto te siguen donde quiera que vaya en matemáticas, al igual que una nube de mosquitos sigue…
Cómo racionalizar un radical de un denominador Una convención de las matemáticas es que usted no deja radicales en el denominador de una expresión cuando se escribe en su forma final. Así que hacemos algo que se llama racionalizar el denominador. Esta convención hace que la recogida como…
Cómo reescribir radicales como exponentes Cuando se te da un problema en forma radical, puede ser más fácil si usted reescribir mediante el uso de exponentes racionales - exponentes que son fracciones. Puede volver a escribir cada radical como un exponente mediante el uso de la siguiente…
Tratar con identidades medio-ángulo que involucran radicales Mediante la adición, sustracción, o duplicando medidas de los ángulos, se puede encontrar gran cantidad de valores exactos de las funciones trigonométricas. Por ejemplo, puede utilizar la identidad de medio ángulo cuando el valor exacto de la…
Potencias, raíces y logaritmos para su uso en bioestadística Estas tres operaciones matemáticas - trabajar con potencias, raíces y logaritmos - están todos relacionados con la idea de multiplicación repetida. Estas funciones básicas se utilizan para ayudar a construir fórmulas más complejas.Elevar a…
Preparación ASVAB: Raíces Familiarizarse con las raíces para el ASVAB. Una raíz es lo contrario de un poder o un exponente. Hay clases infinitas de raíces. Tienes el raíz cuadrada, lo que significa " perdición " una base a la segunda POWER- la raíz cúbica, lo que…