Matemáticas normas fundamentales comunes: el sistema de los números reales
Los estudiantes de secundaria deben tener un entendimiento del sistema de números reales para satisfacer las normas fundamentales comunes. los sistema de números reales contiene todos los números que se pueden representar en una recta numérica, incluidos los números racionales e irracionales:
Numeros racionales son números enteros y fracciones. Te encontrarás con números racionales en diversas formas decimales. A pesar de que una decimal periódico (tales 0,33333333 ...) puede no parecer racional, todavía se puede escribir como la fracción 1/3. Decimales de terminación, tales como 0,25, también son racionales y puede ser escrito como una fracción (en este caso, 1/4). Los estudiantes se encuentran con números racionales a partir de jardín de infantes.
Numeros irracionales no se puede escribir como una fracción o una relación. Usted verá con frecuencia los números irracionales en formas decimales que no se pueden escribir como fracciones. Por ejemplo, pi (3,14159 # 133-) es un número irracional que es que no se repite, pero también no puede ser expresado como una fracción. Los estudiantes empiezan a trabajar con números irracionales en el grado 8.
En la escuela secundaria, los estudiantes comienzan a extender las propiedades de exponentes para exponentes racionales. Por su graduación, los estudiantes deben:
Comprender y explicar cómo las propiedades de número entero (número entero) exponentes se extienden a todos los exponentes racionales, incluyendo exponentes fraccionarios, como 12503.01
Expresar radicales en términos de exponentes racionales. Por ejemplo:
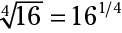
y
Por su graduación, los estudiantes de secundaria también deben ser capaces de explicar las propiedades de los números irracionales y por qué
Adición de dos números racionales resultados en un número racional.
Multiplicando dos números racionales resultados en un número racional.
Adición de dos números irracionales resultados en un número irracional.
Multiplicar un número racional no nulo con un número irracional resultados en un número- irracional por ejemplo, si # 960- es irracional, explique por qué 2 # 960- es irracional.
Una de las mejores maneras de aprender cualquier cosa es tratar de enseñarlo. Cuando su hijo está trabajando con números racionales e irracionales, pídale que definir cada término y explicar la diferencia.
Después de asegurarse de que su hijo tiene una comprensión exacta de estos conceptos, escribir cinco o seis números y la dejó a identificar cuáles son racionales y cuáles son irracionales. Asegúrese de incluir ejemplos de los distintos tipos de decimales.
-
Encuentra representaciones simbólicas de cálculos numéricos con cas -
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 5 - Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 6
- Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 7
- Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 8
- Las normas fundamentales comunes: los estándares de contenido de matemáticas de dominio
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 4 Después de aprender los conceptos básicos de la multiplicación, la división y fracciones en el Grado 3, Grado 4 estudiantes ponen sus habilidades para trabajar por la aplicación de estos conceptos fundamentales comunes a la multi-paso problemas…
9 sistemas numéricos en álgebra para saber LA sistema numérico en álgebra es un conjunto de números - y sistemas de números diferentes se utilizan para resolver diferentes tipos de problemas de álgebra. Sistemas numéricos incluyen los números reales, números naturales, números…
Álgebra II libro para los maniquíes Los exponentes son la abreviatura para la multiplicación repetida. Las reglas para las operaciones que involucran exponentes realizar permiten cambiar las expresiones de multiplicación y división con la misma base en algo más sencillo trabajar…
Cómo convertir fracciones a decimales Puede convertir todas las fracciones a decimales. Las formas decimales de números racionales cualquiera de los extremos o repiten un patrón. Para convertir fracciones a decimales que acaba de dividir la parte por el fondo - dividir el numerador…
Trabajar con ecuaciones radicales y racionales en álgebra ii LA radical la ecuación es una que comienza con una raíz cuadrada, raíz cúbica, o alguna otra raíz y se cambia a otra forma para hacer que el proceso de resolución más fácil. LA racional la ecuación es aquella que implica una expresión…
4 series importantes de los números La línea número crece en ambas direcciones positiva y negativa y rellena con una gran cantidad de números en el medio. He aquí un rápido recorrido por cómo los números encajan como un conjunto de sistemas anidados, uno dentro del otro.Un…
Cómo simplificar los números usando la notación científica Cuando se trabaja con números muy grandes o pequeños, se puede ahorrar en tiempo y espacio - y hacer cálculos más fácil - mediante el uso de la notación científica. Como verá, utiliza dos decimales y exponentes de representar estos números…
Cómo visualizar las fracciones en una recta numérica Las fracciones que ayudan a llenar una gran cantidad de los espacios en la línea de números que se encuentren entre los números contables. Por ejemplo, la figura muestra un primer plano de una recta numérica de 0 a 1.Esta línea número que…
Conceptos básicos de álgebra necesarios para pre-cálculo Los fundamentos de la pre-cálculo consisten en la revisión de los sistemas de numeración, las propiedades de los sistemas numéricos, orden de las operaciones, la notación, y algunas fórmulas esenciales utilizados en gráficos de coordenadas.…
Conceptos básicos de cómo adivinar y comprobar raíces reales Puede utilizar el teorema de la raíz racional para restringir la búsqueda de las raíces de los polinomios. Si bien la regla de los signos de Descartes sólo se estrecha hacia abajo las raíces reales en positivo y negativo, el teorema de la raíz…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo adivinar y comprobar raíces reales - 1 - lista de todas las posibles raíces racionales Cuando usted busca todo lo posible raíces racionales de cualquier polinomio, el primer paso es utilizar el teorema de la raíz racional para mencionarlos a todos.El teorema de la raíz racional dice que si usted toma todos los factores de la…