9 sistemas numéricos en álgebra para saber

LA sistema numérico en álgebra es un conjunto de números - y sistemas de números diferentes se utilizan para resolver diferentes tipos de problemas de álgebra. Sistemas numéricos incluyen los números reales, números naturales, números enteros, enteros, números racionales, números irracionales, números pares y los números impares.

• Numeros reales: Los números reales comprenden el espectro completo de los números. Cubren toda la gama y pueden tomar cualquier forma - fracciones o números enteros, decimales o sin puntos decimales. La gama completa de los números reales incluye decimales que puede seguir para siempre. Los números reales son diferentes de los números imaginarios o complejos.

• Números naturales: Un número natural es un número que es algo natural. ¿Qué números usaste primero? Recuerde que alguien pregunta: "¿Cuántos años tienes?" Usted orgullo levantó cuatro dedos y dijo: "¡Cuatro!" Los números naturales son mayores que cero, pero no incluyen fracciones: 1, 2, 3, 4, 5, 6, 7, y así sucesivamente, hasta el infinito. Utiliza los números naturales a contar objetos y hacer listas.

• Los números enteros: Los números enteros son sólo todos los números naturales, más un cero: 0, 1, 2, 3, 4, 5, y así sucesivamente, hasta el infinito. Actúan como los números naturales y se utilizan cuando se requieren cantidades enteros (no fracciones). Zero también puede indicar ninguna.

  Problemas algebraicos menudo requieren que redondear la respuesta al número entero más cercano. Esto tiene mucho sentido cuando el problema involucra a personas, vehículos, animales, casas, o cualquier cosa que no debe ser cortado en pedazos.

• Enteros: Los enteros incorporan todos los números enteros y sus opuestos (o aditivos inversas de los números enteros). Los enteros pueden ser descritos como siendo números enteros y 0 positivos y negativos:. . . -3, -2, -1, 0, 1, 2, 3,. . . .

  Los enteros son populares en álgebra. Cuando se resuelve un largo y complicado problema y llegar a un número entero, se puede ser feliz porque su respuesta es probablemente correcto. Después de todo, no es una fracción! Esto no quiere decir que las respuestas en el álgebra no pueden ser fracciones o decimales. Es sólo que la mayoría de los libros de texto y libros de referencia tratan de seguir con respuestas agradables para aumentar el nivel de comodidad y evitar confusiones.

• Numeros racionales: Los números racionales son números que actúan racionalmente! En este caso, actuando racionalmente significa que el equivalente decimal del número racional se comporta. El decimal termina en algún lugar, o tiene un patrón de repetición a la misma. Eso es lo que constituye "comportarse". Algunos ejemplos de números racionales con decimales que terminan incluyen 2, 3.4, 5,77623 y -4,5.

  Algunos ejemplos de números racionales con decimales que se repiten el mismo patrón incluyen los siguientes:

  

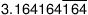
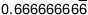
  (La barra horizontal sobre el 164 y el 6 le permite saber que estos números se repiten siempre.) En todos los casos, los números racionales se pueden escribir como una fracción. Todos ellos tienen una fracción que son iguales a.

• Numeros irracionales: Los números irracionales son números reales que no son números racionales. Un número irracional no puede ser escrito como una fracción, y los valores decimales de los irracionales no tener fin y nunca tiene un buen patrón para ellos. Por ejemplo, pi, con sus cifras decimales interminables, es irracional.

• Imaginary / números complejos: Un número que no es real puede ser imaginaria o compleja. Un número imaginario contiene algún múltiplo de yo, que es la siguiente:

  

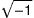
  Por ejemplo, 2 + 3yo es un número complejo.

• Incluso números: Un número par es uno que divide uniformemente por 2, tal como 2, 4, 18, y 352.

• Numeros impares: Un número impar es uno que no divide uniformemente por 2, por ejemplo, 1, 3, 27 y 485.