Preparación núcleo Praxis: cómo encontrar factores de números enteros
Usted tendrá que saber cómo encontrar factores de números enteros para el examen de matemáticas Praxis Core. LA factor de un número entero es un número entero que puede ser dividido en ella un número entero de veces. Por ejemplo, 4 es un factor de 20, ya 4 puede ser multiplicado por el número total 5 (que es también un factor de 20) para obtener 20.
El número 4 no es un factor de 21, 19, o cualquier otro número que no es divisible por 4. Y si se puede romper el factor de un número aún más en sus propios factores, los factores más pequeñas también son factores del número original que empezó. Por ejemplo, debido 2 es un factor de 4, 2 es también un factor de 20.
Cada número entero tiene en sí y 1 para factores. Si esos son los dos únicos factores de un número, que es un numero primo. Por ejemplo, 3, 17, 31, y 79 son números primos.
Para determinar los factores de un número, en primer lugar determinar un factor y lo que tiene que ser multiplicado por conseguir el número. A continuación, busque los factores de los números de la misma manera. Continuar el proceso hasta que no los números se pueden desglosar aún más.
En este punto, usted ha encontrado el factorización prima del número - una representación del número como un producto de todos sus factores primos. A partir de ahí, todos los factores del número, que no sean 1, se puede encontrar multiplicando cada combinación posible de los factores primos.
Encuentra todos los factores de 30.
(A) 30 y 1
(B) 2, 3, y 5
(C) 1, 2, 3, 5, 6, 10, 15, y 30
(D) 2, 3, 5, 6, 10, y 15
(E) 2 y 15
La respuesta correcta es la opción (C). Todos los números listados o son factores primos de 30, los productos de las combinaciones de esos factores primos, o 1. Sin embargo, la opción (C) es la única opción que incluye a todos ellos.
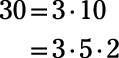
El número 1 es un factor de 30 porque 30 es un número entero, y cada número entero es un factor de sí mismo. Los factores primos de 30 son 5, 2, y 3. Al multiplicar las combinaciones de esos números, los otros factores se pueden determinar.
5 x 2 = 10- 10 x 3 = 30
5 x 3 = 15 15 x 2 = 30
2 x 3 = 6 x 5 6- = 30
-
¿Cómo trabajar con los factores y vectores numéricos en modelos r y cálculos -
Comando Factor de la TI-Nspire CAS álgebra submenú - Diferenciar entre gcfs y lcms en matemáticas núcleo común
-
Cómo factores y múltiplos están relacionados de matemáticas básico común -
Funciones del alfabeto en el álgebra -
Cómo escribir descomposición en factores primos de números compuestos
La identificación de los números primos Un número primo es un número entero mayor que el número 1 que puede ser dividido uniformemente solamente por sí mismo y 1. El primero y el más pequeño número primo es el número 2. Es la única aun número primo. Todos los números primos…
Factores y múltiplos El concepto de divisibilidad - por ejemplo, 12 es divisible por 3, porque 12/3 = 4, sin resto - también puede ser descrito mediante las palabras factor y múltiple. Cuando se trabaja con números positivos, el factor es siempre el número menor y…
Cómo descomponer un número en sus factores primos Cada número es el producto de un conjunto único de factores primos, un grupo de números primos (incluyendo repeticiones) que, cuando se multiplica juntos, es igual a ese número. Usted puede encontrar los factores primos de un número dado,…
¿Cómo encontrar los factores de un número Los factores de un número son todos esos números que pueden dividir uniformemente en el número sin resto. El mayor factor de un número es el número en sí, por lo que siempre se puede enumerar todos los factores de cualquier número porque…
¿Cómo encontrar el máximo común divisor los máximo común divisor (GCF) de un conjunto de números es el mayor número que es un factor de todos esos números. Por ejemplo, el MCD de los números 4 y 6 es 2 porque 2 es el mayor número que es un factor de dos 4 y 6. Aquí aprenderás dos…
¿Cómo encontrar el mínimo común múltiplo los minimo común multiplo (LCM) de un conjunto de números es el número positivo menor que es un múltiplo de cada número en ese conjunto. Por ejemplo, el LCM de los números 2, 3, y 5 es 30 porque30 es un múltiplo de 2 (2 # 183- 15 = 30)30 es…
¿Cómo generar una serie de factores Cuando un número es divisible por un segundo número, ese segundo número es un factor de la primera. Por ejemplo, 10 es divisible por 2, por lo que 2 es un factor de 10.Una buena manera de encontrar todos los factores de un número es mediante la…
¿Cómo generar múltiplos Aunque múltiplos tienden a ser los números más grandes que los factores, la mayoría de los estudiantes encuentran más fáciles de trabajar. Encontrar todos los factores es posible debido a factores de un número son siempre menor o igual al…
Cómo identificar números primos (y compuestos) Cada número contando mayor que 1 es un número primo o un número compuesto. LA numero primo tiene exactamente dos factores - 1 y el número mismo. Por ejemplo, el número 5 es primo porque sus dos únicos factores son 1 y 5. Una número compuesto…
Preparación ASVAB: factores Asegúrese de conocer los factores cuando se va a tomar el ASVAB. LA factor es simplemente un número que se multiplica para obtener un producto. Factoring un número significa tomar el número de diferencia. Es algo así como la multiplicación a…
Preparación ASVAB: múltiplos menos comunes El ASVAB probablemente tendrá preguntas que preguntan por múltiplos comunes. LA común múltiplo es un número que es un múltiplo de dos o más números. Por ejemplo, 20, 30 y 40, son múltiplos comunes de los números 5 y 10.los minimo común…
Preparación ASVAB: cómo simplificar fracciones Simplificar (o reducir) fracciones significa hacer la fracción tan simple como sea posible. Generalmente, usted está obligado a simplificar fracciones en las subpruebas de matemáticas ASVAB antes de poder seleccionar la respuesta correcta.Por…