Funciones del alfabeto en el álgebra

Aquí están algunos funciones del alfabeto

, llamado así porque se nombran usando letras del alfabeto griego. En álgebra, una función es una norma o relación que se define utilizando diversos operadores matemáticos. Y un partido de clasificación adicional es que una función puede tener sólo un valor de salida para cada valor de entrada en su dominio.

Por ejemplo, la función de F (X) = X² + 2X - 3 tiene F (3) = 12 y F (-4) = 5. Cada vez que ingresa un número para el X, usted consigue uno y sólo uno de los resultados de ese número. Esto es especial, y es lo que hace F (X) Una función.

Matemáticas está lleno de muchas funciones reconocibles: funciones lineales, funciones cuadráticas, funciones polinómicas, funciones exponenciales, funciones logarítmicas, funciones seno, funciones hiperbólicas, y así sucesivamente. Pero también hay muchas, muchas funciones que se utilizan en matemáticas, estadística, la física y otras ciencias.

Función de Sigma

La función sigma se utiliza en el estudio de la teoría de números y otras aplicaciones donde es necesario contar con los divisores de un entero.

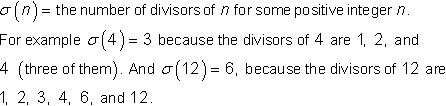
Hay todo tipo de patrones interesantes y teoremas que involucran la función sigma. Uno de los patrones o reglas más rápidas y más fáciles de explicar es

dónde p es un número primo. Todos los números primos tienen sólo dos divisores. Así

y así sucesivamente, para todos los números primos.

Función gamma

La función gamma se relaciona con la función factorial, pero en realidad puede hacer más. Recordemos que n! es el producto de todos los enteros positivos hasta e incluyendo n. Así que si F (n) = n!, después

Esta es una función maravillosa y es más útil en probabilidad y aplicaciones estadísticas. Sin embargo, los valores de entrada de F tienen que ser enteros positivos. La función gamma permite la entrada de los números reales y complejos a excepción de los números enteros negativos y 0. La función gamma es

¡Un pedazo de la torta! Sólo para dar una muestra de algunos de los resultados de la función gamma:

Función Delta

La función delta, o la función delta de Kronecker, se encuentran de forma natural en muchas aplicaciones de ingeniería, la física y las matemáticas. Esta función requiere dos entradas, yo y j, y está definido por una expresión a trozos:

Así

Todas las funciones deben ser tan fácil de calcular!

Función de Eta

La función eta, eta o función de Dirichlet, está definida por una serie alternante y se calcula con la siguiente:

Así que cuando s = 4, usted tiene

que converge a un número cercano a 0.947.

Función de Omega

La función omega está cerca en la definición a la función sigma. Cuando la función sigma cuenta todos los divisores de un número entero, la función omega cuenta sólo los factores primos. Hay dos versiones de la función omega: la función omega sencilla y la función omega grande.

Por ejemplo,

Tiene tres factores primos distintos y un total de 5 factores primos. Así

Función Pi

La función pi también se conoce como el función de conteo de primera. Indica cuántos números primos son menores que el valor de entrada. Así

porque cuatro números primos son más pequeñas que 10: 2, 3, 5, y 7. Y

porque 25 números primos son más pequeños que 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73 , 79, 83, 89, y 97.

Función Mu

La función mu, o función M # 246-bius, es importante en la teoría de números y combinatoria. Es otra función a trozos, la asignación de valores de la función en base a los factores primos de un entero particular que es de entrada. Aquí está la regla:

Considere los números 6, 30 y 18. Las factorizaciones de los números son

6 = 2 # 183-3, 30 = 2 # 183-3 # 183-5, y 18 = 2 # 183-3².

El número 6 no tiene factores primos cuadrados y un número par de factores primos. El número 30 no tiene factores primos cuadrados y un número impar de factores primos. Y el número 18 tiene el factor cuadrado 3². Así