¿Cómo encontrar el máximo común divisor
los máximo común divisor
Conteúdo
Método 1: Utilizar una lista de factores para encontrar el MCD
Este método para encontrar el MCD es más rápido cuando usted está tratando con números más pequeños. Para encontrar el MCD de un conjunto de números, una lista de todos los factores de cada número. El mayor factor que aparece en todas las listas es el MCD. Por ejemplo, para encontrar el MCD de 6 y 15, primera lista de todos los factores de cada número.
Factores de 6: 1, 2, 3, 6
Factores de 15: 1, 3, 5, 15
Debido a que 3 es el mayor factor que aparece en ambas listas, 3 es el MCD de 6 y 15.
Como otro ejemplo, supongamos que usted desea encontrar el MCD de 9, 20 y 25. Empiece haciendo una lista de los factores de cada uno:
Factores de 9: 1, 3, 9
Factores de 20: 1, 2, 4, 5, 10, 20
Los factores de 25: 1, 5, 25
En este caso, el único factor que aparece en las tres listas es 1, por lo que 1 es el MCD de 9, 20 y 25.
Método 2: Utilizar factorización prima para encontrar el GCF
Puede utilizar factorización prima para encontrar el MCD de un conjunto de números. A menudo, esto funciona mejor para un gran número, en las listas de generación de todos los factores pueden llevar mucho tiempo.
Aquí es cómo encontrar el MCD de un conjunto de números usando factorización prima:
Enumerar los factores primos de cada número.
Círculo cada factor primo común - que es, cada factor primordial que es un factor de cada número en el conjunto.
Multiplica todos los números dentro de círculos.
El resultado es la formación bruta de capital.
Por ejemplo, supongamos que usted desea encontrar el MCD de 28, 42 y 70. Paso 1 dice a la lista de los factores primos de cada número. Paso 2 le dice a la vuelta de cada factor primordial que es común a los tres números (como se muestra en la siguiente figura).
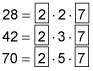
Como se puede ver, los números 2 y 7 son factores comunes de los tres números. Multiplique estos números dentro de círculos juntos:
2 # 183- 7 = 14
Por lo tanto, el MCD de 28, 42 y 70 es 14.
Saber cómo encontrar el MCD de un conjunto de números es importante a la hora de comenzar la reducción de fracciones a su mínima expresión.
¿Cómo reducir fracciones usando factorización prima Puede utilizar factorización prima para reducir fracciones. Comience con sólo números y luego añadir variables (letras que representan cualquier número real) a la mezcla. La belleza de la utilización del método de factorización prima es que…
Cómo escribir descomposición en factores primos de números compuestos Primer factorización le muestra la única manera que un número puede ser un factor. El proceso de descomposición en factores primos se descompone un número compuesto en los números primos que, cuando se multiplica juntos, le dan ese número…
La identificación de los números primos Un número primo es un número entero mayor que el número 1 que puede ser dividido uniformemente solamente por sí mismo y 1. El primero y el más pequeño número primo es el número 2. Es la única aun número primo. Todos los números primos…
Factores y múltiplos El concepto de divisibilidad - por ejemplo, 12 es divisible por 3, porque 12/3 = 4, sin resto - también puede ser descrito mediante las palabras factor y múltiple. Cuando se trabaja con números positivos, el factor es siempre el número menor y…
Cómo descomponer un número en sus factores primos Cada número es el producto de un conjunto único de factores primos, un grupo de números primos (incluyendo repeticiones) que, cuando se multiplica juntos, es igual a ese número. Usted puede encontrar los factores primos de un número dado,…
¿Cómo encontrar los factores de un número Los factores de un número son todos esos números que pueden dividir uniformemente en el número sin resto. El mayor factor de un número es el número en sí, por lo que siempre se puede enumerar todos los factores de cualquier número porque…
¿Cómo encontrar el mínimo común múltiplo los minimo común multiplo (LCM) de un conjunto de números es el número positivo menor que es un múltiplo de cada número en ese conjunto. Por ejemplo, el LCM de los números 2, 3, y 5 es 30 porque30 es un múltiplo de 2 (2 # 183- 15 = 30)30 es…
¿Cómo generar una serie de factores Cuando un número es divisible por un segundo número, ese segundo número es un factor de la primera. Por ejemplo, 10 es divisible por 2, por lo que 2 es un factor de 10.Una buena manera de encontrar todos los factores de un número es mediante la…
Cómo identificar números primos (y compuestos) Cada número contando mayor que 1 es un número primo o un número compuesto. LA numero primo tiene exactamente dos factores - 1 y el número mismo. Por ejemplo, el número 5 es primo porque sus dos únicos factores son 1 y 5. Una número compuesto…
Cómo utilizar las raíces de un polinomio para encontrar sus factores los factor de teorema indica que usted puede ir y venir entre las raíces de un polinomio y los factores de un polinomio. En otras palabras, si usted conoce uno, ya sabes el otro. A veces, su maestro o su libro de texto pueden pedirle que factorizar…
Preparación ASVAB: factores Asegúrese de conocer los factores cuando se va a tomar el ASVAB. LA factor es simplemente un número que se multiplica para obtener un producto. Factoring un número significa tomar el número de diferencia. Es algo así como la multiplicación a…
Preparación ASVAB: múltiplos menos comunes El ASVAB probablemente tendrá preguntas que preguntan por múltiplos comunes. LA común múltiplo es un número que es un múltiplo de dos o más números. Por ejemplo, 20, 30 y 40, son múltiplos comunes de los números 5 y 10.los minimo común…