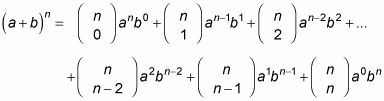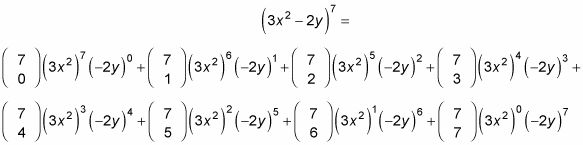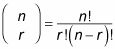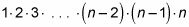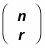Cómo expandir una binomial cuya monomios tienen coeficientes o se elevado a una potencia
A veces, monomios pueden tener coeficientes y / o ser elevado a una potencia antes de comenzar la expansión binomial. En este caso, hay que levantar todo el monomio a la potencia adecuada en cada paso. Por ejemplo, así es como se expande la expresión (3X2 - 2y)7:
Escriba la expansión binomial utilizando el teorema del binomio, sustituyendo en las variables cuando sea necesario.
En caso de haber perdido, aquí está el teorema del binomio:
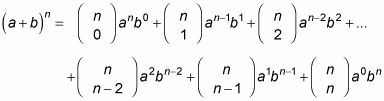
Vuelva a colocar la carta la en el teorema con la cantidad (3X2) Y la letra b con (-2y). No deje que los coeficientes o exponentes te asuste - usted todavía está sustituirlos en el teorema del binomio. Reemplazar n con 7. Se termina con
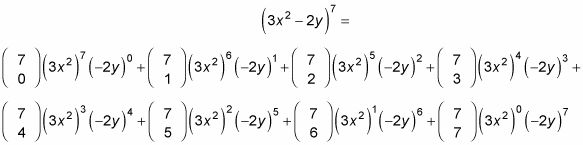
Encuentra los coeficientes binomiales.
La fórmula para la expansión binomial se escribe de la siguiente forma:
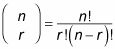
Usted puede recordar el término factorial de sus clases de matemáticas anteriores. Si no, aquí es un recordatorio: n!, cuyo texto es el "n factorial", se define como
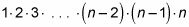
Ahora, de vuelta al problema. Utilizando la fórmula de combinación que da la siguiente:
Reemplaza todo
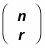
con los coeficientes de la Etapa 2.
1 (3X2)7(-2y)0 + 7 (3X2)6(-2y)1 + 21 (3X2)5(-2y)2 + 35 (3X2)4(-2y)3 + 35 (3X2)3(-2y)4 + 21 (3X2)2(-2y)5 + 7 (3X2)1(-2y)6 + 1 (3X2)0(-2y)7
Levante los monomios a los poderes especificados para cada término.
1 (2,187x14) (1) + 7 (729x12) (- 2y) + 21 (243x10) (4y2) + 35 (81x8) (- 8y3) + 35 (27x6) (16y4) + 21 (9x4) (- 32y5 ) + 7 (3x2) (64y6) + 1 (1) (- 128y7)
Simplifique.
2,187x14 - 10,206x12y + 20,412x10y2 - 22,680x8y3 + 15,120x6y4 - 6,048x4y5 + 1,344x2y6 - 128y7
Cómo distribuir binomios Cuando distribuye en álgebra, se multiplica cada uno de los términos dentro del paréntesis por otro término que se encuentra fuera de los paréntesis. Así que, cuando distribuya un binomio largo de varios términos, que acaba de aplicar el…
Cómo aumentar los poderes de poderes Al elevar una potencia a una potencia en una expresión exponencial, se encuentra el nuevo poder de multiplicar los dos poderes juntos. Por ejemplo, en la siguiente expresión, X a la potencia de 3 está siendo elevado a la potencia de 6, y así…
¿Cómo reconocer un binomio perfectamente cuadrado Reconociendo un binomio perfectamente cuadrado puede hacer la vida más fácil. Cuando reconoces perfectamente cuadrado binomial, que haya identificado un atajo que ahorra tiempo al distribuir binomios sobre otros términos.Cuando el mismo binomio…
Cómo romper una diferencia cúbica o la suma Después de que se haya registrado para ver si hay un máximo común divisor (MCD) de un polinomio dado y descubrió que es un binomio que no es una diferencia de cuadrados, se debe considerar que puede ser una diferencia o suma de cubos.LA…
Cómo expandir un binomio cuya monomios no tienen coeficientes o exponentes Los resultados finales de una expansión binomial dependen de si el monomio original tenía no hay coeficientes o exponentes (excepto 1) de las variables. Para encontrar la expansión de binomios con el teorema en una situación básica, siga estos…
Cómo expandir un binomio que contiene números complejos El tipo más complicado de la expansión binomial implica el número complejo yo, porque no sólo está tratando con el teorema del binomio, pero se trata de números imaginarios también. Al subir los números complejos a una potencia, tenga en…
¿Cómo encontrar coeficientes binomiales Dependiendo del número de veces que se debe multiplicar el mismo binomio - un valor también conocido como exponente - los coeficientes binomiales para que exponente particular, son siempre los mismos. Los coeficientes binomiales se encuentran…
¿Cómo adivinar y comprobar raíces reales - 3 - raíces de pruebas por polinomios dividen usando división sintética Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división sintética. División…
Cómo escribir un sistema en forma de matriz En un sistema de ecuaciones lineales, donde cada ecuación está en la forma Hacha + Por + Cz + . . . = K, puede representar los coeficientes de este sistema en la matriz, llamada matriz de coeficientes. Si todas las variables se alinean entre sí…
Cómo utilizar el teorema de la energía acorde acordes El Teorema de acordes-acordes de potencia se llama así por el hecho de que utiliza un acorde y - puede adivinar? - Otro acorde!Acorde-Acorde Poder Teorema: Si dos cuerdas de un círculo se cruzan, entonces el producto de las medidas de las partes…
Encontrar probabilidades binomiales con una fórmula Aquí, se llega a practicar la búsqueda de probabilidades binomiales usando una fórmula. Los siguientes problemas tienen una variable aleatoria binomial con p = 0.55. Utilice las siguientes fórmulas para la distribución binomial para los…
¿Cómo encontrar probabilidades binomiales utilizando una fórmula estadística Después de identificar que una variable aleatoria X tiene una distribución binomial, es probable que desee encontrar probabilidades para X. La buena noticia es que usted no tiene que encontrarlos a partir del rasguño se llega a utilizar fórmulas…