¿Cómo adivinar y comprobar raíces reales - 3 - raíces de pruebas por polinomios dividen usando división sintética

Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división sintética. División sintética es un acceso directo para larga división de polinomios. Es un caso especial de división cuando el divisor es un factor lineal de la forma X + c, dónde c es una constante.

Por desgracia, el acceso directo sólo funciona si el divisor (X + c) Es un familiar de primer grado binomial con un coeficiente principal de 1 (que siempre se puede hacer más 1 dividiendo todo por el coeficiente principal primero). Por suerte, siempre se puede utilizar la división sintética para averiguar si una posible raíz es en realidad una raíz.

Estos son los pasos generales de división sintética:

1. Asegúrese de que el polinomio está escrito en orden descendente.

   El término con el mayor exponente es lo primero.

2. Anote los coeficientes y la constante del polinomio de izquierda a derecha, rellenando un cero términos de forma de cualquier grado que son lugar missing- la raíz que está probando fuera del signo de división sintética.

   El signo de división se parece a los lados izquierdo e inferior de un rectángulo. Deje espacio por debajo de los coeficientes de escribir otra fila de números.

3. Déjate caer el primer coeficiente por debajo del signo de división.

4. Multiplique la raíz que está probando por el número que acaba de caer hacia abajo y escribir la respuesta a continuación el siguiente coeficiente.

5. Añadir el coeficiente y producto de la Etapa 4 y poner el resultado debajo de la línea.

6. Multiplique la raíz que está probando con la respuesta del Paso 5 y poner el producto por debajo del siguiente coeficiente.

7. Continúe multiplicando y sumando hasta que utilice el último número dentro del signo de división sintética.

   Si obtiene un resto, el número al que la prueba no es una raíz.

   Si la respuesta es 0, ¡enhorabuena! Usted ha encontrado una raíz. Los números por debajo de la señal de división sintética son los coeficientes del polinomio cociente. El grado de este polinomio es uno menos que el original (el dividendo), por lo que el exponente en la primera X plazo debe ser uno menos de lo que empezó.

Digamos que usted probar las raíces de la ecuación, F(X) = 2X⁴ - 9X³ - 21X² + 88X + 48, y se han eliminado X = 2 usando la división larga, para que sepa que no empezar por ahí. Por lo tanto, usted decide hacer división sintética, como se muestra en la figura para X = 4.

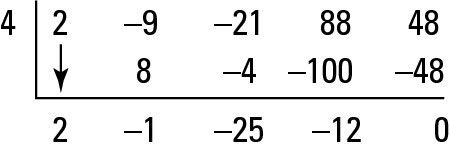
El 4 en el exterior en la figura es la raíz que está probando. Los números en el interior son los coeficientes del polinomio. Aquí está el proceso de síntesis, paso a paso:

1. El 2 por debajo de la línea justo cae por debajo de la línea anterior.

2. Multiplique 4 con 2 para obtener 8 y escribir que en virtud de la próxima legislatura, -9.

3. Añadir -9 + 8 para obtener -1.

4. Multiplique 4 con -1 para obtener -4, y escribir que bajo el -21.

5. Añadir -21 + -4 conseguir -25.

6. Multiplique 4 con -25 para obtener -100, y escribir que bajo 88.

7. Añadir 88--100 conseguir -12.

8. Multiplique 4 con -12 para obtener -48, y escribir que bajo 48.

9. Añadir 48--48 para obtener 0.

Todo lo que hacemos es multiplicar y sumar, por lo que la división sintética es el acceso directo. El último número, 0, es su resto. Debido a que usted obtiene un residuo de 0, X = 4 es una raíz.

Los otros números son los coeficientes del cociente, en orden desde el más alto grado para el menos- sin embargo, el cociente es siempre un grado menor que el grado del polinomio originales. Así que el cociente en este ejemplo es 2X³ - X² - 25X - 12.

Cada vez que una raíz funciona, siempre se debe probar automáticamente de nuevo en la respuesta cociente para ver si es una raíz doble, usando el mismo proceso. LA raíz doble se produce cuando un factor tiene una multiplicidad de dos. A raíz doble es un ejemplo de la multiplicidad. Usted prueba X = 4 otra vez, como se muestra en la figura.

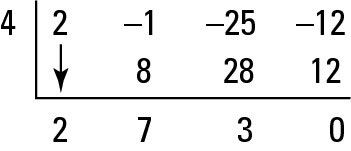
Whaddya saber? Usted obtiene un residuo de 0 otra vez, así X = 4 es una raíz doble. (En términos matemáticos, usted dice que X = 4 es una raíz con multiplicidad de dos.) Usted tiene que comprobar de nuevo, sin embargo, para ver si tiene una multiplicidad superior. Cuando división sintética X = 4 una vez más, que no funciona. La siguiente figura ilustra este fracaso. Debido a que el resto no es 0, X = 4 no es una raíz de nuevo.

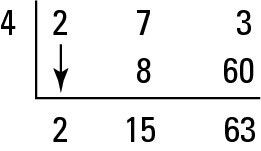
Trabaje siempre fuera el más nuevo cociente cuando se utiliza la división sintética. De esta manera, el grado pone más y más hasta que terminan con una expresión cuadrática, o hasta que haya agotado todas las posibles raíces racionales. Si una expresión cuadrática permanece, puede resolver la ecuación cuadrática utilizando técnicas como el factoring, completando el cuadrado, o la fórmula cuadrática.

Antes de la prueba X = 4 por última vez, el polinomio (llamado polinomio deprimido) Bajó a un segundo grado: 2X² + 7X + 3. Si se toma esta expresión, se obtiene (2X + 1) (X + 3). Esto le da dos más raíces de -1/2 y -3. Para resumirlo todo, has encontrado X = 4 (dos multiplicidad), X = -1/2, Y X = -3. Encontraste cuatro raíces complejas - dos de ellos son los números reales negativos, y dos de ellos son números reales positivos.

los Teorema del Resto dice que el resto se obtiene cuando se dividir un polinomio por un binomio es el mismo que el resultado que se obtiene de enchufar el número en el polinomio. Por ejemplo, cuando se utiliza el algoritmo de división para dividir por X - 2, que estaba probando para ver si X = 2 es una raíz. Podrías haber utilizado división sintética para hacer esto, porque usted todavía consigue un resto de 100. Y si el enchufe 2 en F(X) = 2X⁴ - 9X³ - 21X² + 88X + 48, usted también consigue 100.