¿Cómo adivinar y comprobar raíces reales - 2 - raíces de pruebas por polinomios en división usando la división larga
Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división larga de polinomios y la esperanza de que cuando se divide obtener un resto de 0. Una vez que tenga una lista de posibles raíces racionales, a continuación, elegir uno y asume que es una raíz.
Por ejemplo, considere la ecuación F(X) = 2X4 - 9X3 - 21X2 + 88X + 48, que tiene las siguientes posibles raíces racionales:
Si X = c es una raíz, después X - c es un factor. Así que si tienes que elegir X = 2 como su conjetura de la raíz, X - 2 debe ser un factor. Puede utilizar la división larga para probar si X - 2 es en realidad un factor y, por lo tanto, X = 2 es una raíz.
La división de polinomios para obtener una respuesta concreta no es algo que se hace todos los días, pero la idea de una función o expresión que se escribe como el cociente de dos polinomios es importante para la pre-cálculo. Si divide un polinomio por otro y obtener un residuo de 0, el divisor es un factor, que a su vez da una raíz.
En la jerga de las matemáticas, el algoritmo de división afirma lo siguiente: Si F(X) Y d(X) Son polinomios tales que d(X) No es igual a 0, y el grado de d(X) No es mayor que el grado de F(X), Hay polinomios únicas q(X) Y r(X) de tal manera que
En la llanura Inglés, el dividendo es igual a la del divisor cociente más el resto. Siempre se puede ver sus resultados por recordar esta información.
Recuerde que el recurso mnemotécnico DIRTY Monkeys Smell Banuncio al hacer la división larga para revisar sus raíces. Asegúrese de que todos los términos del polinomio se enumeran en orden descendente y que se representa cada grado. En otras palabras, si X2 no se encuentra, poner en un marcador de posición de 0X2 y luego hacer la división. (Este paso es sólo para hacer más fácil el proceso de división.)
Para dividir dos polinomios, siga estos pasos:
Divide.
Divida el término principal del dividendo por el término principal del divisor. Escribe este cociente directamente encima del plazo que acaba de dividir en.
Multiply.
Multiplique el término cociente del paso 1 por todo el divisor. Escribe este polinomio bajo el dividendo de manera que los términos como se alinean.
Subtract.
Reste toda la línea que acaba de escribir del dividendo.
Usted puede cambiar todos los signos y añadir, si eso te hace sentir más cómodo. De esta manera, usted no olvidará signos.
Bllamar por la próxima legislatura.
No exactamente lo que este dice- derribar la próxima legislatura en el dividendo.
Repita los pasos 1-4 y otra vez hasta el polinomio resto tiene un grado que es menor que el dividendo de.
La lista siguiente explica cómo dividir 2X4 - 9X3 - 21X2 + 88X + 48 por X - 2. Cada paso se corresponde con el paso numerado en la ilustración en esta figura.
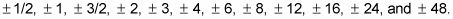
(Tenga en cuenta que el uso de la regla de los signos de Descartes, usted encontrará que este ejemplo particular puede tener raíces positivas, por lo que es eficaz para tratar un número positivo aquí. Si la regla de los signos de Descartes había dicho que no existían raíces positivas, usted no probar ningún positivos !)
Divide.
¿Qué tienes que multiplicar X en el divisor de para hacer que se convierta en 2X4 en el dividendo? El cociente, 2X3, va por encima del 2X4 término.
Multiply.
Multiplique este cociente por el divisor y escribir debajo del dividendo.
Subtract.
Restar esta línea del dividendo: (2X4 - 9X3) - (2X4 - 4X3) = -5X3. Si lo has hecho bien el trabajo, la sustracción de los primeros términos siempre produce 0.
Banillo hacia abajo.
Derriba los otros términos del dividendo.
Divide.
¿Qué tienes que multiplicar X por hacerla -5X3? Ponga la respuesta, -5X2, por encima de la -21X2.
Multiply.
Multiplique el -5X2 veces el X - 2, para poder -5X3 + 10X2. Escribe debajo el resto con los grados alineados.
Subtract.
Ahora tiene (-5X3 - 21X2) - (-5X3 + 10X2) = -31X2.
Banillo hacia abajo.
El 88X toma su lugar.
Divide.
Lo que hay que multiplicar por hacer X convertido -31X2? El cociente -31X pasa por encima de -21X2.
Multiply.
El valor -31X veces (X - 2) -31X2 + 62X- escribirlo bajo el resto.
Subtract.
Ahora tiene (-31X2 + 88X) - (-31X2 + 62X), Que es 26X.
Banillo hacia abajo.
El 48 se reduce.
Divide.
El término 26X Dividido por X es 26. Esta respuesta va en la parte superior.
Multiply.
La constante de 26 multiplicado por (X - 2) es 26X - 52.
Subtract.
Usted resta (26X + 48) - (26X - 52) para obtener 100.
Scima.
El resto 100 tiene un grado que es menor que el divisor de X - 2.
Guau . . . ahora ya sabes por qué lo llaman largo división. Usted pasó por todo eso para saber que X - 2 no es un factor del polinomio, lo que significa que X = 2 no es una raíz.
Si se divide por c y el resto es 0, entonces la expresión lineal (X - c) Es un factor y que c es una raíz. Un resto distinto de 0 implica que (X - c) No es un factor y que c no es una raíz.
Conceptos básicos de cómo adivinar y comprobar raíces reales Puede utilizar el teorema de la raíz racional para restringir la búsqueda de las raíces de los polinomios. Si bien la regla de los signos de Descartes sólo se estrecha hacia abajo las raíces reales en positivo y negativo, el teorema de la raíz…
Cómo calcular salidas para funciones racionales En pre-cálculo, se puede calcular salidas para funciones racionales. LA función racional es una función que se puede expresar como el cociente de dos polinomios, de tal manera quedonde el grado de q(X) Es mayor que cero.Estos son los pasos a…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo encontrar un factor común más grande de un polinomio No importa cuántos términos de un polinomio tiene, uno siempre quiere comprobar si hay un máximo común divisor (MCD) en primer lugar. Si el polinomio tiene un GCF, factoring el resto del polinomio es mucho más fácil porque una vez que se toma…
¿Cómo encontrar raíces imaginarias usando el teorema fundamental del álgebra El teorema fundamental del álgebra puede ayudarle a encontrar las raíces imaginarias. Raíces imaginarias aparecerá en una ecuación de segundo grado cuando el discriminante de la ecuación de segundo grado - la parte bajo el signo de la raíz…
¿Cómo encontrar las raíces reales de un polinomio utilizando la regla de los signos de Descartes Si sabe el número de raíces totales un polinomio tiene, puede utilizar un teorema muy bien llamada Regla de los signos de Descartes a contar cuántas raíces son números reales (tanto positivos y negativa) y cuántos son imaginarios. Usted ve, el…
Cómo graficar polinomios Aunque puede parecer desalentador, graficar polinomios es un proceso bastante sencillo. Una vez que haya encontrado los ceros de un polinomio, puede seguir unos sencillos pasos para representarla gráficamente.Por ejemplo, si ha encontrado los ceros…
Cómo graficar polinomios cuando las raíces son números imaginarios - una visión general En pre-cálculo y en el cálculo, ciertas funciones polinómicas tener raíces no reales además de raíces reales (y algunas de las funciones más complicadas tener todas raíces imaginarias). Cuando usted debe encontrar tanto, empezar por la…
¿Cómo adivinar y comprobar raíces reales - 3 - raíces de pruebas por polinomios dividen usando división sintética Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división sintética. División…
¿Cómo adivinar y comprobar raíces reales - 1 - lista de todas las posibles raíces racionales Cuando usted busca todo lo posible raíces racionales de cualquier polinomio, el primer paso es utilizar el teorema de la raíz racional para mencionarlos a todos.El teorema de la raíz racional dice que si usted toma todos los factores de la…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
Cómo utilizar las raíces de un polinomio para encontrar sus factores los factor de teorema indica que usted puede ir y venir entre las raíces de un polinomio y los factores de un polinomio. En otras palabras, si usted conoce uno, ya sabes el otro. A veces, su maestro o su libro de texto pueden pedirle que factorizar…