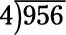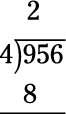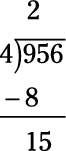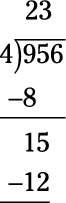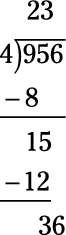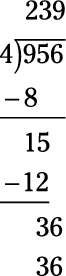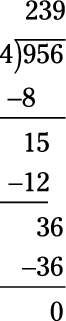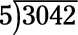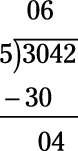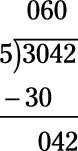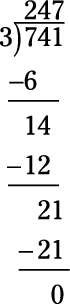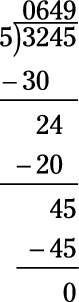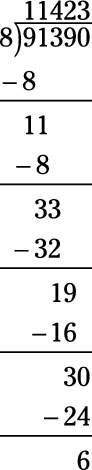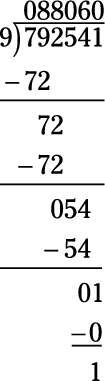Cómo dividir grandes números con la división larga
Para dividir números más grandes, use Larga division.
A diferencia de los otros cuatro grandes operaciones, la división larga se mueve de izquierda a derecha. Para cada dígito en el
dividendo (el número que está dividiendo), que completan un ciclo de división, multiplicación y resta.
En algunos problemas, el número en la parte inferior del problema no es un 0. En estos casos, la respuesta tiene una resto, que es una pieza sobrante que debe tenerse en cuenta. En esos casos, se escribe r seguido de cualquier número que sobra.
Ejemplos de preguntas
Divida 956/4.
239. Comience escribiendo el problema así:
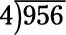
Para empezar, se preguntan cuántas veces 4 entra en 9 - es decir, lo que es 9.4? La respuesta es 2 (con un poco de sobra), por lo que escribir 2 directamente sobre el 9. Ahora multiplique 2 x 4 para obtener 8, coloque el producto directamente debajo del 9, y dibuja una línea debajo de él:
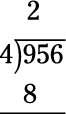
Reste 9-8 para obtener 1. (Nota: Después de restar, el resultado debe ser menor que el divisor (en este problema, el divisor es 4). Luego bajar el siguiente número (5) para hacer el nuevo número 15.
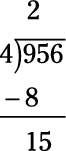
Estos pasos son un ciclo completo. Para completar el problema, sólo tiene que repetir. Ahora se preguntan cuántas veces 4 entra en 15 - es decir, lo que es 15/4? La respuesta es 3 (con un poco de sobra). Así que escribir el 3 por encima del 5, y luego multiplicar 3 x 4 para obtener 12. Escribir el producto bajo 15.
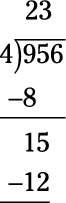
Reste 15 a 12 para obtener 3. Luego bajar el siguiente número (6) para hacer el nuevo número 36.
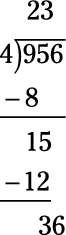
Otro ciclo se completa, por lo que comienza el próximo ciclo preguntando cuántas veces 4 entra en 36 - es decir, lo que es 36/4? La respuesta esta vez es 9. Anote 9 por encima del 6, multiplicar 9 x 4, y coloque esta por debajo del 36.
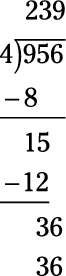
Ahora restar 36-36 = 0. Debido a que usted no tiene más números para derribar, haya terminado, y la respuesta (es decir, el cociente) Es el número más alto de el problema:
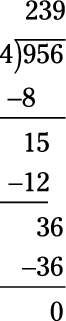
Divida 3042/5.
608 r 2. Comience escribiendo el problema así:
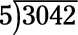
Para empezar, pregunte cuántas veces 5 entra en 3. La respuesta es 0 - 5, porque no entra en 3 - por lo que escribir 0 por encima del 3. Ahora tiene que hacer la misma pregunta con el primero de dos dígitos del divisor: ¿Cuántas veces 5 ir a 30 - es decir, lo que es 30/5? La respuesta es 6, por lo que coloque el 6 por encima del 0. Así es como para completar el primer ciclo:
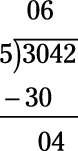
A continuación, se preguntan cuántas veces 5 entra en 4. La respuesta es 0 - 5, porque no entra en 4 - Así que escribir un 0 por encima de la 4. Ahora derrocar al siguiente número (2), para hacer el número 42:
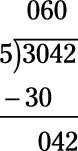
Pregunte cuántas veces 5 entra en 42 - es decir, lo que es 42/5? La respuesta es 8 (con un poco más de la izquierda), así completar el ciclo de la siguiente manera:

Debido a que usted no tiene más números para derribar, estás acabado. La respuesta (cociente) está en la cima del problema (que puede caer el 0), y el resto está en el fondo del problema. Así 3042/5 = 608 con un resto de 2. Para ahorrar espacio, escribir esta respuesta como 608 r 2.
Preguntas de práctica
Divida 741/3.
Evalúe 3245/5.
Averiguar 91.390 / 8.
Encontrar 792.541 / 9.
Las siguientes son las respuestas a las preguntas de la práctica:
247
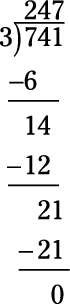
649
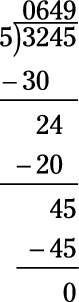
11423 r 6
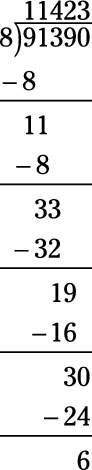
88060 r 1
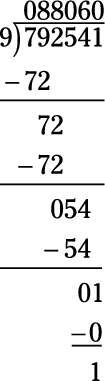
Sobre el autor
 Cómo dividir decimales
Cómo dividir decimales Cuando usted sabe cómo hacer una división larga, averiguar cómo dividir decimales es fácil. Sin embargo, a diferencia de la división de números enteros, decimales, hay que añadir ceros en el dividendo y también hay que completar el problema…
 Cómo dividir con un resto
Cómo dividir con un resto División es diferente de la suma, resta y multiplicación en que tener un resto es posible. Un resto es simplemente una porción sobrante de la división. Por ejemplo, supongamos que usted es un padre de un picnic con sus tres hijos. Has traído a…
 Cómo hacer una división larga por un número
Cómo hacer una división larga por un número En los viejos tiempos, sabiendo cómo dividir un gran número era importante. División larga básica sigue siendo bueno saber, por lo que los siguientes ejemplos le mostrarán cómo dividir un divisor de un dígito a otro número, y luego cómo…
 Cómo multiplicar y dividir números negativos
Cómo multiplicar y dividir números negativos Multiplicar y dividir números negativos es básicamente lo mismo que sucede con los números positivos. La presencia de uno o más signos menos (-) no cambia la parte numérica de la respuesta. La única pregunta es si el signo de la respuesta es…
 Cómo multiplicar decimales
Cómo multiplicar decimales Multiplicar decimales es diferente de la suma y resta en que usted no tiene que preocuparse de alinear los puntos decimales. De hecho, la única diferencia entre la multiplicación de números enteros y decimales viene al final.Aquí es cómo…
 Los paréntesis y la propiedad asociativa
Los paréntesis y la propiedad asociativa Paréntesis operaciones del grupo en conjunto, que le dice que hacer ninguna operación dentro de un conjunto de paréntesis antes de usted hace operaciones fuera de ella. Los paréntesis pueden hacer una gran diferencia en el resultado que se…
 Potencias y raíces cuadradas
Potencias y raíces cuadradas Elevar un número a una poder es una forma rápida de multiplicar un número por sí mismo. Por ejemplo, 25, que se lee como dos a la quinta potencia, significa que multiplica 2 por sí mismo 5 veces:25 = 2 x 2 x 2 x 2 x 2 = 32El número 2 se llama…
 ¿Cómo adivinar y comprobar raíces reales - 2 - raíces de pruebas por polinomios en división usando la división larga
¿Cómo adivinar y comprobar raíces reales - 2 - raíces de pruebas por polinomios en división usando la división larga Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división larga de polinomios y la…
 ¿Cómo adivinar y comprobar raíces reales - 3 - raíces de pruebas por polinomios dividen usando división sintética
¿Cómo adivinar y comprobar raíces reales - 3 - raíces de pruebas por polinomios dividen usando división sintética Una vez que haya utilizado el teorema de la raíz racional para enumerar todos los posibles raíces racionales de cualquier polinomio, el siguiente paso es poner a prueba las raíces. Una forma es utilizar la división sintética. División…
 Cómo bidmas pueden ayudar a superar las pruebas de aritmética
Cómo bidmas pueden ayudar a superar las pruebas de aritmética BIDMAS significa 'corchetes, índices, dividir, multiplicar, sumar, restar "y le indica el orden en el que hay que hacer una suma complicado. (Índices, por cierto, son pequeños números por encima ya la derecha de un número, así: 142. Lo que…
 Actualice sus habilidades básicas de matemáticas mulitiplication y división
Actualice sus habilidades básicas de matemáticas mulitiplication y división La capacidad de multiplicar y dividir números enteros son matemáticas habilidades básicas que necesitará al tomar cualquier prueba de aritmética. Multiplicar y dividir son realmente sólo agregando repetida y restando: 4 + 4 es el mismo que 4 x…
 Preparación ASVAB: cómo multiplicar y dividir decimales
Preparación ASVAB: cómo multiplicar y dividir decimales El ASVAB contiene dos subpruebas de matemáticas. Usted inevitablemente se encontrará con decimales, así que asegúrese de que está preparado y saber cómo multiplicar y dividir decimales y, así como realizar otras operaciones cuando sea…