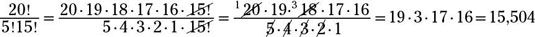Cómo simplificar expresiones factoriales
Conjuntos de elementos tienen operaciones especiales utilizados para combinarlos o cambiarlos. Otra operación que se utiliza con conjuntos (pero que no es exclusivo de juegos) es factorial,
denotado por el signo de exclamación.Utilice la operación factorial en las fórmulas utilizadas para contar el número de elementos de la unión, intersección, o complemento de conjuntos. Factoriales aparecen en las fórmulas que utiliza para contar los elementos de los conjuntos que son realmente grandes.
La operación factorial, n!, Se define como n! = n(n - 1) (n - 2) (n - 3) # 183- # 183- # 183- 4 # 183- 3 # 183- 2 # 183- 1. En otras palabras, se multiplica el número de n, que está operándose, por cada número entero positivo más pequeño que n. Algunos valores de n! son: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120, 6! = 720, y así sucesivamente. Usted ve que están consiguiendo bastante grande muy rápido.
Otro valor factorial que usted necesita es 0! = 1. Usted puede pensar que es un error tipográfico. Nope. Por definición, 0 factorial es igual a 1. Es una de esas cosas extravagantes que los matemáticos declaran y hacen que todo el mundo el uso de manera que las respuestas a los problemas salen bien. La gente quería las fórmulas para contar para ser consistente para todos los números utilizados.
Simplificar factoriales no es difícil, pero no es tan fácil como usted puede pensar a primera vista. Simplificar
que no sólo puede reducir el 6 y el 3. Usted tiene que mirar todos los factores que intervienen en cada operación factorial. Escriba los factoriales, y se obtiene
Ahora reducir los factores como y simplificar:
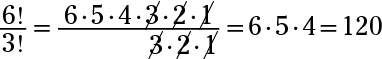
Ejemplo de pregunta
Simplifique la expresión factorial:
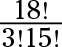
816. En primer lugar, escribir las expansiones de los factoriales. ¡Pero espera! (Tenga en cuenta que a pesar de los signos de exclamación, el factorial no funciona en la palabra espera.) En lugar de escribir todos los factores de 18 !, acaba de escribir 18! como 18 # 183- 17 # 183- 16 # 183- 15 !. Usted decide parar con el 15 a causa de la 15! en el denominador.
El 15! términos se anulan, así que no se moleste en escribir todos esos términos idénticos en el numerador y el denominador:
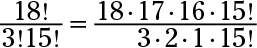
Ahora dividir a cabo cualesquiera otros factores comunes y simplificar:
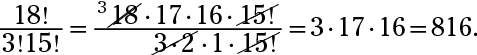
Preguntas de práctica
Simplifique la expresión:
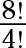
Simplifique la expresión:
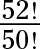
Simplifique la expresión:
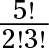
Simplifique la expresión:
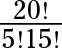
A continuación se presentan las respuestas a las preguntas de la práctica:
La respuesta es 1.680.
Expandir el numerador, y dejar el denominador como 4 !. Luego de reducir y simplificar:
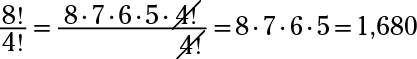
La respuesta es 2.652.
Expandir el numerador, y dejar el denominador como 50 !. Luego de reducir y simplificar:
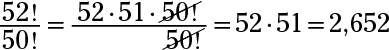
La respuesta es 10.
Expandir el numerador y el primer factor en el denominador. Reducir los factores comunes y simplificar:
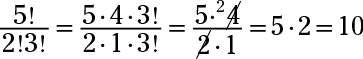
La respuesta es 15.504.
Expandir el numerador y el primer factor en el denominador. Reducir los factores comunes y simplificar:
-
¿Cómo evaluar los factoriales en la TI-84 Plus -
Cómo multiplicar tres números mixtos -
1.001 de matemáticas y de práctica pre-álgebra problemas básicos para los maniquíes - Consejos de matemáticas básicas: fracciones
-
Cómo aumentar y reducir los términos de las fracciones -
Cómo multiplicar dos fracciones y reducir la respuesta
Cómo multiplicar fracciones ¿Por qué no todo en la vida ser tan fácil como la multiplicación de fracciones? Para multiplicar dos fracciones, simplemente hacer lo siguiente: Multiplique los dos numeradores (números superiores) para obtener el numerador de la respuesta-…
Cómo reducir una fracción a su mínima expresión Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá reducido términos en comparación con el otro. Puede que tenga que reducir los términos de las fracciones…
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
Cómo restar fracciones con diferentes denominadores Cuando quiera restar fracciones con diferentes denominadores, usted tiene una opción de métodos: el camino más fácil, el truco rápido, y la manera tradicional.La manera fácil siempre funciona, y usted debe utilizar este método para la mayor…
Cómo restar fracciones con denominadores comunes Como con la adición, restando fracciones que tienen el mismo denominador (también llamado común denominador) Es muy simple: sólo resta el segundo numerador de la primera y mantener el denominador de la misma. En algunos casos, es posible que…
Simplificar y factorizar expresiones En álgebra, la simplificación y factoring expresiones son procesos opuestos. Simplificar una expresión a menudo significa eliminación un par de parentheses- factorizar una expresión a menudo significa aplicar ellos.Supongamos que comienza con…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
Cómo expandir un binomio que contiene números complejos El tipo más complicado de la expansión binomial implica el número complejo yo, porque no sólo está tratando con el teorema del binomio, pero se trata de números imaginarios también. Al subir los números complejos a una potencia, tenga en…
Cómo racionalizar un radical de un denominador Una convención de las matemáticas es que usted no deja radicales en el denominador de una expresión cuando se escribe en su forma final. Así que hacemos algo que se llama racionalizar el denominador. Esta convención hace que la recogida como…
Cambie de senos y cosenos en una identidad trigonometría Con algunas identidades trigonométricas, usted puede decidir para simplificar las cosas, ya sea cambiando todo para senos y cosenos o factoring a cabo alguna función. A veces, no está claro de qué lado usted debe trabajar en o lo que debe hacer…
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
Cómo multiplicar por un conjugado de encontrar una identidad trigonometría Conjugados ofrecen una gran manera de encontrar identidades trigonométricas. En matemáticas, un conjugado formado por los mismos dos términos como la primera expresión, separados por el signo opuesto. Por ejemplo, el conjugado deEn trig,…