¿Cómo encontrar la distribución de muestreo de una proporción de la muestra

Si utiliza un tamaño suficiente gran muestra estadística, se puede aplicar el teorema del límite central (CLT) a una proporción de la muestra para los datos categóricos para encontrar su distribución muestral. los proporción de la población, p, es la proporción de individuos de la población que tienen una determinada característica de interés (por ejemplo, la proporción de todos los estadounidenses que son votantes registrados, o la proporción de todos los adolescentes que son dueños de teléfonos celulares). los proporción de la muestra, denotado

(pronunciado p-hat), Es la proporción de individuos de la muestra que tienen que characteristic- particular, en otras palabras, el número de individuos de la muestra que tienen que característica de interés dividida por el tamaño total de la muestra (n).

Por ejemplo, si se toma una muestra de 100 adolescentes y encontrar 60 de ellos propios teléfonos celulares, la proporción de la muestra de adolescentes de celulares propietaria es

La distribución muestral de

tiene las siguientes propiedades:

• Su media, denotado por

  

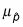
• (pronunciado mu sub-p-hat), Es igual a la proporción de la población, p.

• Su error estándar, denotado por

  

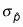
• (digamos sigma sub-p-hat), Es igual a:

  

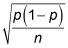
• (Tenga en cuenta que debido a que n se encuentra en el denominador, el error estándar disminuye a medida n aumenta.)

• Debido a la CLT, su forma es aproximadamente normales, siempre que el tamaño de la muestra es lo suficientemente grande. Por lo tanto se puede utilizar la distribución normal para encontrar probabilidades aproximadas para

  

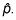
• Cuanto mayor sea el tamaño de la muestra (n) O cuanto más cerca p es 0,50, más cerca la distribución de la proporción de la muestra es a una distribución normal.

Si usted está interesado en el número (en lugar de la proporción) de los individuos en la muestra con la característica de interés, se utiliza la distribución binomial para encontrar probabilidades para sus resultados.

¿Qué tan grande es lo suficientemente grande para la CLT a trabajar para las proporciones de la muestra? La mayoría de los estadísticos de acuerdo en que tanto np y n(1 - p) Debe ser mayor que o igual a 10. Es decir, el número promedio de éxitos (np) Y el número promedio de fallos n(1 - p) debe ser por lo menos 10.

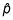
Para ayudar a ilustrar la distribución muestral de la proporción de la muestra, considere una encuesta estudiantil que acompaña a la prueba ACT cada año preguntando si el estudiante le gustaría un poco de ayuda con las habilidades matemáticas. Supongamos (a través de la investigación del pasado) que el 38% de todos los estudiantes que toman el ACT responden que sí. Eso significa p, la proporción de la población, es igual a 0,38 en este caso. La distribución de las respuestas (sí, no) para esta población se muestran en la figura anterior como un gráfico de barras.

Debido a que el 38% se aplica a todos los estudiantes que toman el examen, puede utilizar p para denotar la proporción de la población, en lugar de

que denota proporciones muestrales. Típicamente p es desconocida, pero este ejemplo le da un valor a señalar cómo las proporciones de muestra de las muestras tomadas de la población se comportan en relación con la proporción de la población.

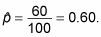
Ahora tome todas las posibles muestras de n = 1.000 estudiantes de esta población y encontrar la proporción en cada muestra que dijeron que necesitan ayuda en matemáticas. La distribución de estas proporciones muestrales se muestra en la figura anterior. Tiene una aproximado distribución normal con media p = 0,38 y error estándar igual a:

(o aproximadamente el 1,5%).

los aproximado distribución normal funciona porque se cumplan las dos condiciones para la CLT:

Y por eso n es tan grande (1000), la aproximación es excelente.