Cómo calcular el margen de error para una proporción de la muestra
Al informar los resultados de una encuesta estadística, es necesario incluir el margen de error. La fórmula general para el margen de error para una proporción de la muestra (si se cumplen ciertas condiciones) es
dónde
es la proporción de la muestra, n es el tamaño de la muestra, y z * es la apropiada z *-valor por su nivel deseado de confianza (de la tabla siguiente).
| z *-Los valores para seleccionadas (Porcentaje) ConfidenceLevels | |
| Porcentaje Confianza | z* -Valor |
|---|---|
| 80 | 1.28 |
| 90 | 1,645 |
| 95 | 1.96 |
| 98 | 2.33 |
| 99 | 2.58 |
Tenga en cuenta que estos valores se toman de la (Z) distribución estándar normal. La zona entre cada valor z * y el negativo de ese valor z * es el porcentaje de confianza (aproximadamente). Por ejemplo, el área entre z * = 1,28 y z = -1.28 es de aproximadamente 0,80. Por lo tanto esta tabla se puede ampliar a otros porcentajes de confianza también. El gráfico muestra sólo los porcentajes de confianza más comúnmente utilizados.
Estos son los pasos para calcular el margen de error para una proporción de la muestra:
Encuentre el tamaño de la muestra, n, y la proporción de la muestra.
La proporción de la muestra
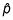
es el número de la muestra con la característica de interés, dividido por n.
Multiplicar la proporción de la muestra por
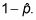
Divida el resultado por n.
Toma la raíz cuadrada del valor calculado.
Ahora tiene el error estándar,
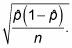
Multiplique el resultado por el adecuado z * -valor para el nivel de confianza deseado.
Consulte la tabla anterior para la adecuada z *-valor. Si el nivel de confianza es del 95%, el z *-valor es 1,96.
He aquí un ejemplo: Supongamos que la última encuesta de la Organización Gallup muestreó a 1.000 personas de los Estados Unidos, y los resultados muestran que 520 personas (52%) creen que el presidente está haciendo un buen trabajo, en comparación con el 48% que no lo cree así. En primer lugar, supongamos que desea un nivel de 95% de confianza, por lo que z * = 1.96. El número de estadounidenses en la muestra que dijeron que aprueban el presidente resultó ser 520. Esto significa que la proporción de la muestra,
es 520/1000 = 0,52. (El tamaño de la muestra, n, era 1000) El margen de error para esta pregunta de sondeo se calcula de la siguiente manera.:
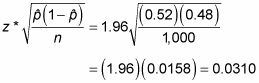
De acuerdo con estos datos, usted concluye con una confianza del 95% que el 52% de los estadounidenses aprueba el presidente, de más o menos 3.1%.
Dos condiciones se deben cumplir para poder utilizar un z *-valor en la fórmula para el margen de error para una proporción de la muestra:
Usted necesita estar seguro de que
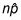
es al menos 10.
Usted necesita asegurarse de que
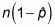
es al menos 10.
En el ejemplo de una encuesta sobre el presidente, n = 1,000,
Ahora compruebe las condiciones:
Ambos números son al menos 10, por lo que todo está bien.
La mayoría de las encuestas que te encuentras se basan en cientos o incluso miles de personas, por lo que el cumplimiento de estas dos condiciones es generalmente un pedazo de pastel (a menos que la proporción de la muestra es muy grande o muy pequeño, lo que requiere un mayor tamaño de muestra para que las condiciones de trabajo).
Una parte de la muestra es la versión decimal del porcentaje de la muestra. En otras palabras, si usted tiene un porcentaje de la muestra de 5%, debe utilizar 0,05 en la fórmula, no 5. Para cambiar un porcentaje en forma decimal, simplemente divida por 100. Después de que todos los cálculos se acaban, puede cambiar de nuevo a un porcentaje al multiplicar su respuesta final en un 100%.
El número de errores típicos que hay que sumar o restar para obtener la MOE depende de la confianza que usted quiere estar en los resultados (esto se llama su nivel de confianza). Por lo general, usted quiere estar cerca del 95% de confianza, por lo que la regla básica es sumar o restar cerca de 2 errores estándar (1,96, para ser exactos) para obtener el MOE (usted consigue esto desde la regla empírica). Esto le permite representan alrededor del 95% de todos los resultados posibles que pueda haber ocurrido con el muestreo repetido. Para 99% de confianza, sumar y restar 2,58 errores estándar. (Esto supone una distribución normal en gran n- . desviación típica conocida) Sin embargo, si se utiliza un porcentaje de confianza más grande, entonces su MOE será más grande - por lo que no es una solución de compromiso.




