¿Cómo afecta al tamaño de la muestra margen de error
En las estadísticas, las dos ideas más importantes en relación con el tamaño de la muestra y margen de error son, en primer lugar, el tamaño de la muestra y margen de error tienen una inversa relación- y la segunda, después de un punto, lo que aumenta el tamaño de la muestra más allá de lo que ya tiene le da una disminuida volver porque el aumento de la precisión será insignificante.
La relación entre el margen de error y tamaño de la muestra es sencillo: Como el tamaño de la muestra aumenta, el margen de error se reduce. Esta relación se llama una inversa porque los dos se mueven en direcciones opuestas. Si lo piensas, tiene sentido que mientras más información tenga, más precisos serán los resultados van a ser (en otras palabras, cuanto menor sea el margen de error será conseguir). (Eso supone, por supuesto, que los datos fueron recolectados y manipulados correctamente.)
Supongamos que la última encuesta de la Organización Gallup muestreó a 1.000 personas de los Estados Unidos, y los resultados muestran que 520 personas (52%) creen que el presidente está haciendo un buen trabajo, en comparación con el 48% que no lo cree así. En primer lugar, supongamos que desea un nivel de 95% de confianza, por lo que encontrar z * usando la siguiente tabla.
| z *-Los valores para seleccionadas (Porcentaje) ConfidenceLevels | |
| Porcentaje Confianza | z* -Valor |
|---|---|
| 80 | 1.28 |
| 90 | 1,645 |
| 95 | 1.96 |
| 98 | 2.33 |
| 99 | 2.58 |
A partir de la tabla, se encuentra que z * = 1.96.
El número de estadounidenses en la muestra que dijeron que aprueban el presidente resultó ser 520. Esto significa que la proporción de la muestra,
es 520/1000 = 0,52. (El tamaño de la muestra, n, era 1000) El margen de error para esta pregunta de sondeo se calcula de la siguiente manera.:
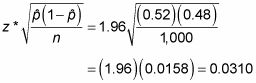
De acuerdo con estos datos, usted concluye con una confianza del 95% que el 52% de los estadounidenses aprueba el presidente, de más o menos 3.1%.
Utilizando la misma fórmula, se puede ver cómo el margen de error cambia dramáticamente para muestras de diferentes tamaños. Supongamos que en la encuesta de la aprobación presidencial que n era 500 en lugar de 1000. Ahora, el margen de error de confianza del 95% es
que es equivalente a 4,38%. Si n se incrementa a 1500, el margen de error (con el mismo nivel de confianza) se convierte
o 2,53%. Finalmente, cuando n = 2000, el margen de error es
o 2,19%.
Teniendo en cuenta estos resultados diferentes, se puede ver que los tamaños de muestra más grandes disminuyen el margen de error, pero después de cierto punto, tiene un retorno disminuida. Cada vez que la encuesta a una persona más, el costo de sus aumentos de la encuesta, y viniendo de un tamaño de muestra de, por ejemplo, 1,500 a un tamaño de muestra de 2.000 disminuye su margen de error de sólo un 0,34% (un tercio del uno por ciento!) - 0,0253 hasta 0,0219. El costo y la molestia extra para conseguir que la pequeña disminución en el margen de error puede no valer la pena. Más grande no siempre es mucho mejor!
-
Análisis exploratorio de datos cuantitativos (eda) técnicas -
La elección de un nivel de confianza de una muestra de población -
Definición y cálculo de margen de error - Sacar conclusiones sobre una población con intervalos de confianza y pruebas de hipótesis
-
Calcular tamaño de la muestra en las estadísticas -
Cómo calcular un intervalo de confianza para una media poblacional cuando se conoce la desviación estándar
Cómo calcular un intervalo de confianza para una media poblacional con una desviación estándar desconocida y / o pequeño tamaño de la muestra Usted puede calcular un intervalo de confianza (IC) para la media o promedio, de una población, incluso si la desviación estándar es desconocida o el tamaño de la muestra es pequeño. Cuando una característica estadística que está siendo…
Cómo calcular el margen de error para una media muestral Cuando una pregunta de investigación pide a encontrar una estadística media de la muestra (o promedio), es necesario reportar un margen de error, o el Ministerio de Educación, para la media de la muestra. La fórmula general para el margen de…
Cómo calcular el margen de error para una proporción de la muestra Al informar los resultados de una encuesta estadística, es necesario incluir el margen de error. La fórmula general para el margen de error para una proporción de la muestra (si se cumplen ciertas condiciones) esdóndees la proporción de la…
Cómo determinar el tamaño mínimo necesario para una muestra estadística El margen de error de un intervalo de confianza (IC) se ve afectada por las dimensiones de la muestra- estadística como el tamaño aumenta, margen de error disminuye. En cuanto a esta a la inversa, si quieres un menor margen de error (y no lo hace…
Cómo determinar el intervalo de confianza para una proporción de la población Usted puede encontrar el intervalo de confianza (IC) para una proporción de la población para mostrar la probabilidad estadística de que es probable que se produzcan dentro de la población de una característica.Cuando una característica que se…
¿Cómo encontrar t *-valores para los intervalos de confianza Intervalos de confianza estimación de los parámetros de población, tales como la media poblacional, mediante el uso de una estadística (por ejemplo, la media de la muestra) más o menos un margen de error. Para calcular el margen de error para…
Cómo interpretar el margen de error en las estadísticas Usted probablemente ha escuchado o visto resultados como este: " Esta encuesta estadística tiene un margen de error de más o menos 3 puntos porcentuales ". ¿Qué significa esto? La mayoría de las encuestas se basan en información obtenida de…
Vinculación de margen de error y la población proporción Las preguntas de práctica aquí tienen que trabajar en el margen de error para los medios de la población y proporciones poblacionales. Resolver los siguientes problemas relacionados con el margen de error y la población proporción.La tabla…
Estadísticamente calcular tamaño de la muestra En el diseño de un estudio, el tamaño de la muestra es una consideración importante, ya que cuanto mayor sea el tamaño de la muestra, más datos que usted tiene, y cuanto más precisos serán los resultados (suponiendo datos de alta calidad). Si…
Estadísticas enigmas: se trata de pacientes que no responden la encuesta No respondedores son siempre un problema cuando se está calculando los resultados de una encuesta. Antes de poder los números de crisis en todas las encuestas que te dan la espalda, usted tiene que decidir qué hacer con las encuestas que no lo…
Estadísticas para los maniquíes Después que los datos se han recogido, el primer paso en el análisis es a crujir algunas estadísticas descriptivas para hacerse una idea de los datos. Por ejemplo:¿Dónde está el centro de datos ubicado?Cómo extendido son los datos?Cómo…
Encuentra tamaños de muestra Con el análisis de clientes, la recogida de datos a partir de una muestra de clientes cuesta mucho menos y toma mucho menos tiempo que la medición de cada cliente. El nivel de precisión que se obtiene de incluso una pequeña muestra suele ser…