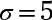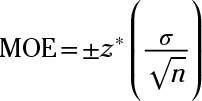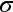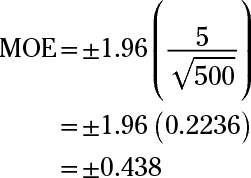Definición y cálculo de margen de error
Un margen de error es el "más o menos" parte hay que añadir a los resultados estadísticos para decirle a todos que usted reconoce que los resultados de las muestras varían de una muestra a otra, y podría variar de la condición real de la población. El margen de error ayuda a indicar cuánto cree esos resultados podrían variar, con un cierto nivel de confianza. Resuelve los siguientes problemas sobre margen de error básico.
La tabla siguiente proporciona el z * - valores para (porcentaje) niveles de confianza seleccionados.
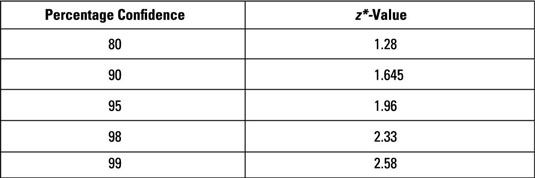
Ejemplos de preguntas
Una encuesta muestra que García lidera Smith en un 54% a 46% con un margen de error de más / menos 5% a un nivel de confianza del 95%.
¿Qué conclusión se puede sacar de esta encuesta?
Responder: La elección es muy reñida.
Usted puede utilizar el sondeo a la conclusión de que el 54% de los votantes en esta muestra votaría por García, y al proyectar los resultados a la población, es añadir un margen de error de más / menos 5%. Eso significa que la votación proporción para García se estima entre 54% - 5% = 49% y 54% + 5% = 59% en la población con 95% de confianza.
También puede utilizar el sondeo a la conclusión de que el 46% de los votantes en esta muestra votaría por Smith, y cuando usted proyecta los resultados a la población, es añadir un margen de error de más / menos 5%. Eso significa que la votación proporción de Smith se estima entre 46% - 5% = 41% y 46% + 5% = 51% en la población con 95% de confianza (sobre muchas muestras).
Intervalo de confianza de García es de 49% a 59%, y el intervalo de confianza de Smith es de 41% a 51%. Debido a que los intervalos de confianza se superponen, la elección es muy reñida.
¿Cuál es el margen de error para la estimación de una media poblacional dado la siguiente información y un nivel de confianza del 95%?
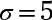
n = 500
Responder: más / menos 0,438
La fórmula para el margen de error en la estimación de una media de la población es
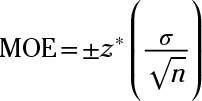
dónde z * es el valor de la tabla para un determinado nivel de confianza (95% en este caso, o 1,96),
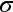
es la desviación estándar de la población (5), y n es el tamaño de la muestra (500).
Ahora, sustituir los valores en la fórmula y resuelve:
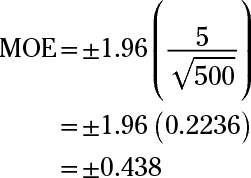
El margen de error para un intervalo de confianza del 95% para la media de la población es más / menos 0,438.
Si necesita más práctica sobre este y otros temas de su curso de estadística, visite 1.001 Estadísticas Entrenamiento Problemas para Dummies comprar acceso en línea a 1.001 problemas de práctica estadísticas! Podemos ayudarle a rastrear su rendimiento, ver dónde se necesita para estudiar y crear un problema personalizado establece para dominar sus habilidades de Estadísticas.
-
Análisis exploratorio de datos cuantitativos (eda) técnicas -
Comprobación de confianza valores críticos de intervalos estadísticos -
Comprobación de fórmulas para los intervalos de confianza - La elección de un nivel de confianza de una muestra de población
- Intervalos de confianza
-
Los intervalos de confianza y las proporciones de población
Sacar conclusiones sobre una población con intervalos de confianza y pruebas de hipótesis Al sacar conclusiones sobre una población a partir de muestras elegidas al azar (un proceso llamado inferencia estadística), Puede utilizar dos métodos: intervalos de confianza y pruebas de hipótesis.Intervalos de confianzaLA intervalo de…
¿Cómo afecta al tamaño de la muestra margen de error En las estadísticas, las dos ideas más importantes en relación con el tamaño de la muestra y margen de error son, en primer lugar, el tamaño de la muestra y margen de error tienen una inversa relación- y la segunda, después de un punto, lo…
Cómo calcular un intervalo de confianza para una media poblacional cuando se conoce la desviación estándar Si conoce la desviación estándar de una población, entonces se puede calcular un intervalo de confianza (IC) para la media o promedio, de esa población. Cuando una característica estadística que está siendo medido (tales como ingresos, IQ,…
Cómo calcular el margen de error para una media muestral Cuando una pregunta de investigación pide a encontrar una estadística media de la muestra (o promedio), es necesario reportar un margen de error, o el Ministerio de Educación, para la media de la muestra. La fórmula general para el margen de…
Cómo determinar el intervalo de confianza para una proporción de la población Usted puede encontrar el intervalo de confianza (IC) para una proporción de la población para mostrar la probabilidad estadística de que es probable que se produzcan dentro de la población de una característica.Cuando una característica que se…
¿Cómo encontrar t *-valores para los intervalos de confianza Intervalos de confianza estimación de los parámetros de población, tales como la media poblacional, mediante el uso de una estadística (por ejemplo, la media de la muestra) más o menos un margen de error. Para calcular el margen de error para…
Cómo interpretar el margen de error en las estadísticas Usted probablemente ha escuchado o visto resultados como este: " Esta encuesta estadística tiene un margen de error de más o menos 3 puntos porcentuales ". ¿Qué significa esto? La mayoría de las encuestas se basan en información obtenida de…
Vinculación de margen de error y la población proporción Las preguntas de práctica aquí tienen que trabajar en el margen de error para los medios de la población y proporciones poblacionales. Resolver los siguientes problemas relacionados con el margen de error y la población proporción.La tabla…
En cuanto a los valores críticos del intervalo de confianza Los valores críticos (z*-valores) son un componente importante de los intervalos de confianza (la técnica estadística para estimar parámetros poblacionales). los z* -valor, que aparece en el margen de la fórmula de error, mide el número de…
Estadísticas para los maniquíes Después que los datos se han recogido, el primer paso en el análisis es a crujir algunas estadísticas descriptivas para hacerse una idea de los datos. Por ejemplo:¿Dónde está el centro de datos ubicado?Cómo extendido son los datos?Cómo…
Topografía intervalos de confianza estadísticos En estadística, un intervalo de confianza es una conjetura acerca de algunas características de la población. Un intervalo de confianza contiene un plus estimación o menos un inicial margen de error (la cantidad que usted espera que sus…
Terminología utilizada en las estadísticas Al igual que todos los temas, las estadísticas tienen su propio idioma. El lenguaje es lo que ayuda a que sabes lo que es un problema está pidiendo, ¿qué se necesitan los resultados, y cómo describir y evaluar los resultados de una manera…