Cómo calcular un intervalo de confianza para una media poblacional cuando se conoce la desviación estándar
Si conoce la desviación estándar de una población, entonces se puede calcular un intervalo de confianza (IC) para la media o promedio, de esa población. Cuando una característica estadística que está siendo medido (tales como ingresos, IQ, precio, talla, cantidad o peso) es numérica, la mayoría de la gente quiere estimar la media (promedio) de valor para la población. Usted calcula la media poblacional,
mediante el uso de una media de la muestra,
más o menos un margen de error. El resultado se denomina una intervalo de confianza para la media poblacional,
Cuando se conoce la desviación estándar de la población, la fórmula para un intervalo de confianza (CI) para una media de la población es
desviación, n es el tamaño de la muestra, y z * representa la apropiada z*-valor de la distribución normal estándar para su nivel de confianza deseado.
| z*-valores para los distintos niveles de confianza | |
| Nivel de confianza | z * -valor |
|---|---|
| 80% | 1.28 |
| 90% | 1.645 (por convenio) |
| 95% | 1.96 |
| 98% | 2.33 |
| 99% | 2.58 |
El cuadro anterior muestra los valores de z * para los niveles de confianza dado. Tenga en cuenta que estos valores se toman de la (Z) distribución estándar normal. La zona entre cada valor z * y el negativo de ese valor z * es el porcentaje de confianza (aproximadamente). Por ejemplo, el área entre z * = 1,28 y z = -1.28 es de aproximadamente 0,80. Por lo tanto esta tabla se puede ampliar a otros porcentajes de confianza también. El gráfico muestra sólo los porcentajes de confianza más comúnmente utilizados.
En este caso, los datos o bien tienen que venir de una distribución normal, o si no, entonces n tiene que ser lo suficientemente grande (por lo menos 30 o menos) para que el teorema del límite central a aplicar, lo que permite utilizar z * -valores en la fórmula.
Para calcular un IC para la media (promedio) de la población, en estas condiciones, haga lo siguiente:
Determinar el nivel de confianza y encontrar el adecuado z *-valor.
Consulte la tabla de arriba.
Encuentra la media de la muestra
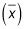
para el tamaño de la muestra (n).
Nota: La desviación estándar de la población se supone que es un valor conocido,
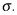
Multiplicar z * veces
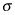
y dividir que por la raíz cuadrada de n.
Este cálculo le da el margen de error.
Llevar
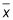
más o menos el margen de error para obtener el CI.
El extremo inferior de la IC es
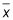
menos el margen de error, mientras que el extremo superior de la CI es
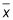
más el margen de error.
Por ejemplo, supongamos que usted trabaja para el Departamento de Recursos Naturales y desea estimar, con un 95% de confianza, la media (promedio) longitud de todos los alevines de lucioperca en una charca criadero de peces.
Porque quieres un intervalo de confianza del 95%, su z *-valor es 1,96.
Supongamos que usted toma una muestra aleatoria de 100 alevines y determinar que la longitud media es de 7,5 pulgadas- asumir la desviación estándar de población es de 2,3 pulgadas. Esto significa
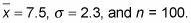
Multiplicar 1,96 veces 2,3 dividido por la raíz cuadrada de 100 (que es 10). El margen de error es, por lo tanto,
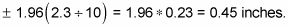
Su intervalo de confianza del 95% para la longitud media de alevines de lucioperca en esta charca criadero de peces es
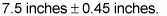
(El extremo inferior del intervalo es de 7,5 - 0,45 = 7,05 pulgadas- el extremo superior es de 7,5 + 0,45 = 7,95 pulgadas).
Después de calcular un intervalo de confianza, asegúrese de que siempre interpreta con palabras un no-estadístico entendería. Es decir, hablar de los resultados en términos de lo que la persona en el problema es tratar de averiguar - los estadísticos llaman a esto la interpretación de los resultados " en el contexto del problema ". En este ejemplo, usted puede decir: " con 95% de confianza, la duración media de alevines de lucioperca en todo este estanque criadero de peces es de entre 7,05 y 7,95 pulgadas, basado en mis datos de la muestra ". (Siempre asegúrese de incluir las unidades apropiadas.)




